2019版高考數(shù)學(xué)二輪復(fù)習(xí) 第1篇 專題5 立體幾何學(xué)案

《2019版高考數(shù)學(xué)二輪復(fù)習(xí) 第1篇 專題5 立體幾何學(xué)案》由會(huì)員分享，可在線閱讀，更多相關(guān)《2019版高考數(shù)學(xué)二輪復(fù)習(xí) 第1篇 專題5 立體幾何學(xué)案（3頁(yè)珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。

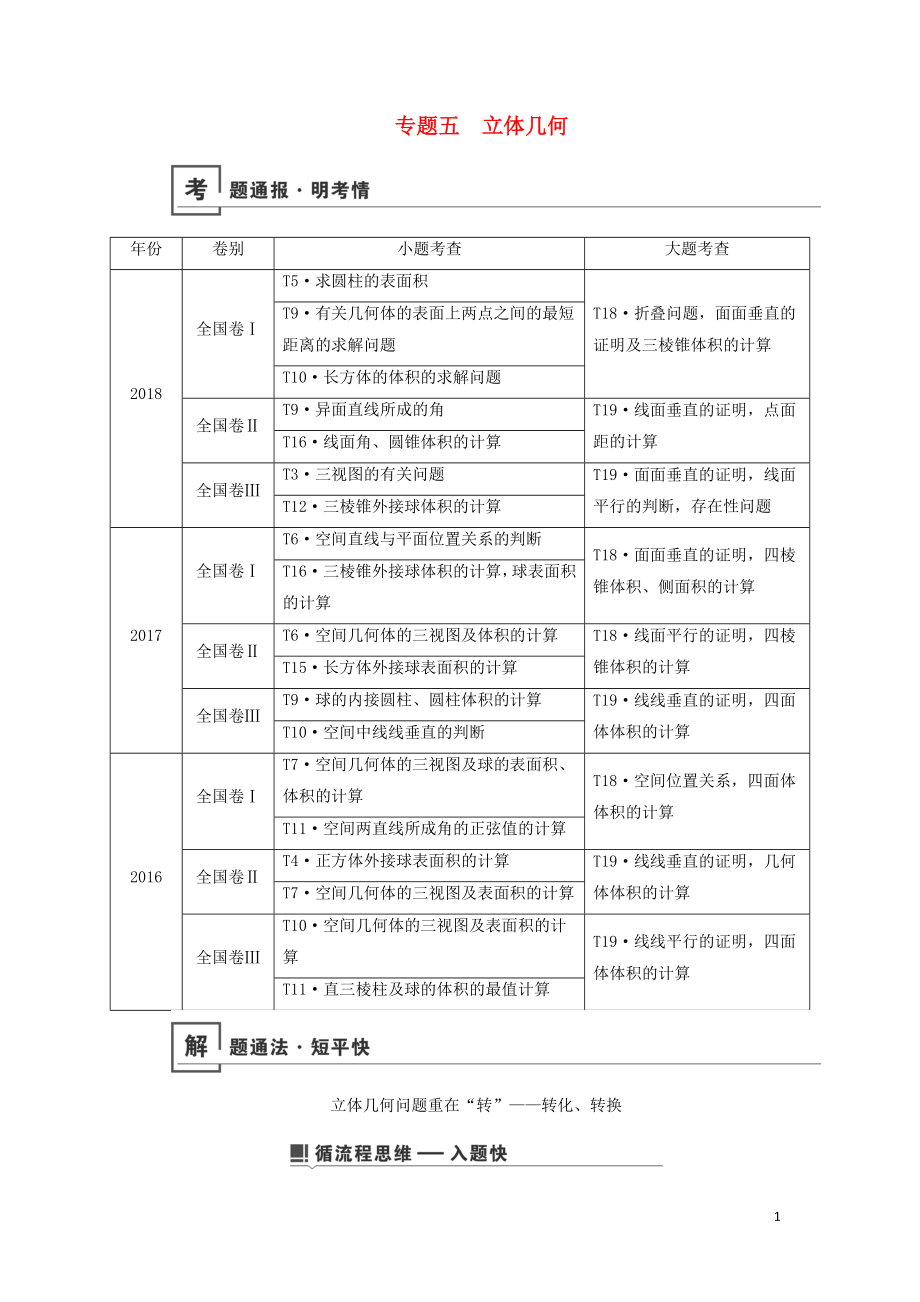
1、專題五　立體幾何 年份 卷別 小題考查 大題考查 2018 全國(guó)卷Ⅰ T5·求圓柱的表面積 T18·折疊問(wèn)題，面面垂直的證明及三棱錐體積的計(jì)算 T9·有關(guān)幾何體的表面上兩點(diǎn)之間的最短距離的求解問(wèn)題 T10·長(zhǎng)方體的體積的求解問(wèn)題 全國(guó)卷Ⅱ T9·異面直線所成的角 T19·線面垂直的證明，點(diǎn)面距的計(jì)算 T16·線面角、圓錐體積的計(jì)算 全國(guó)卷Ⅲ T3·三視圖的有關(guān)問(wèn)題 T19·面面垂直的證明，線面平行的判斷，存在性問(wèn)題 T12·三棱錐外接球體積的計(jì)算 2017 全國(guó)卷Ⅰ T6·空間直線與平面位置關(guān)系的判斷 T18·面面垂直的證明，四棱錐體積、側(cè)面積的

2、計(jì)算 T16·三棱錐外接球體積的計(jì)算，球表面積的計(jì)算 全國(guó)卷Ⅱ T6·空間幾何體的三視圖及體積的計(jì)算 T18·線面平行的證明，四棱錐體積的計(jì)算 T15·長(zhǎng)方體外接球表面積的計(jì)算 全國(guó)卷Ⅲ T9·球的內(nèi)接圓柱、圓柱體積的計(jì)算 T19·線線垂直的證明，四面體體積的計(jì)算 T10·空間中線線垂直的判斷 2016 全國(guó)卷Ⅰ T7·空間幾何體的三視圖及球的表面積、體積的計(jì)算 T18·空間位置關(guān)系，四面體體積的計(jì)算 T11·空間兩直線所成角的正弦值的計(jì)算 全國(guó)卷Ⅱ T4·正方體外接球表面積的計(jì)算 T19·線線垂直的證明，幾何體體積的計(jì)算 T7·空間幾何體的三視圖及表面積的

3、計(jì)算 全國(guó)卷Ⅲ T10·空間幾何體的三視圖及表面積的計(jì)算 T19·線線平行的證明，四面體體積的計(jì)算 T11·直三棱柱及球的體積的最值計(jì)算 立體幾何問(wèn)題重在“轉(zhuǎn)”——轉(zhuǎn)化、轉(zhuǎn)換 立體幾何解答題的基本模式是論證推理與計(jì)算相結(jié)合，以某個(gè)幾何體為依托，分步設(shè)問(wèn)，逐層加深，解決這類題目的原則是轉(zhuǎn)化、轉(zhuǎn)換．轉(zhuǎn)化——空間平行關(guān)系間的轉(zhuǎn)化、垂直關(guān)系間的轉(zhuǎn)化、平行與垂直關(guān)系間的轉(zhuǎn)化以及平面幾何與立體幾何的轉(zhuǎn)化等；轉(zhuǎn)換——對(duì)幾何體的體積、錐體體積考查頂點(diǎn)轉(zhuǎn)換，多面體體積多分割轉(zhuǎn)換為幾個(gè)規(guī)則幾何體的體積和或體積差來(lái)求解，求體積時(shí)距離與體積計(jì)算的轉(zhuǎn)換等． 【典例】　如圖，四棱錐P-A

4、BCD中，PA⊥底面ABCD，AD∥BC，AB＝AD＝AC＝3，PA＝BC＝4，M為線段AD上一點(diǎn)，AM＝2MD，N為PC的中點(diǎn)． (1)證明MN∥平面PAB； (2)求四面體N-BCM的體積． [解題示范]　(1)證明：由已知得AM＝AD＝2． 取BP的中點(diǎn)T，連接AT，TN，由N為PC的中點(diǎn)知TN∥BC，TN＝BC＝2． 又AD∥BC，故TN綊AM， 所以四邊形AMNT為平行四邊形，于是MN∥AT． 因?yàn)镸N?平面PAB，AT?平面PAB，所以MN∥平面PAB?． (2)解：因?yàn)镻A⊥平面ABCD，N為PC的中點(diǎn)，所以N到平面ABCD的距離為PA． 取BC中點(diǎn)E，

5、連接AE． 由AB＝AC＝3得AE⊥BC，AE＝＝． 由AM∥BC得M到BC的距離為， 故S△BCM＝×4×＝2． 所以四面體N-BCM的體積 VN-BCM＝×S△BCM×＝.? ?轉(zhuǎn)化：平行關(guān)系間的轉(zhuǎn)化．線∥線?線∥面．TN∥BC，AD∥BC?TN綊AM?MN∥AT?MN∥平面PAB． ?轉(zhuǎn)換：距離與體積的計(jì)算轉(zhuǎn)換． 點(diǎn)面距、點(diǎn)線距?體積的計(jì)算． AE＝?點(diǎn)M到BC的距離為；點(diǎn)N到平面ABCD的距離為PA?四面體N-BCM的體積． 立體幾何的內(nèi)容在高考中的考查情況總體上比較穩(wěn)定，因此，復(fù)習(xí)備考時(shí)往往有“綱”可循，有“題”可依．在平時(shí)的學(xué)習(xí)中，要重視識(shí)圖訓(xùn)練，能正確確定關(guān)鍵點(diǎn)或線的位置，將局部空間問(wèn)題轉(zhuǎn)化為平面模型．其中，平行、垂直關(guān)系的判定與性質(zhì)是立體幾何的核心內(nèi)容；空間距離、面積與體積的計(jì)算是重點(diǎn)內(nèi)容． 3