2013年中考數(shù)學(xué)知識(shí)點(diǎn) 四邊形專題專練 四邊形的認(rèn)識(shí)與證明單元綜合檢測(cè)題

《2013年中考數(shù)學(xué)知識(shí)點(diǎn) 四邊形專題專練 四邊形的認(rèn)識(shí)與證明單元綜合檢測(cè)題》由會(huì)員分享，可在線閱讀，更多相關(guān)《2013年中考數(shù)學(xué)知識(shí)點(diǎn) 四邊形專題專練 四邊形的認(rèn)識(shí)與證明單元綜合檢測(cè)題（5頁(yè)珍藏版）》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。

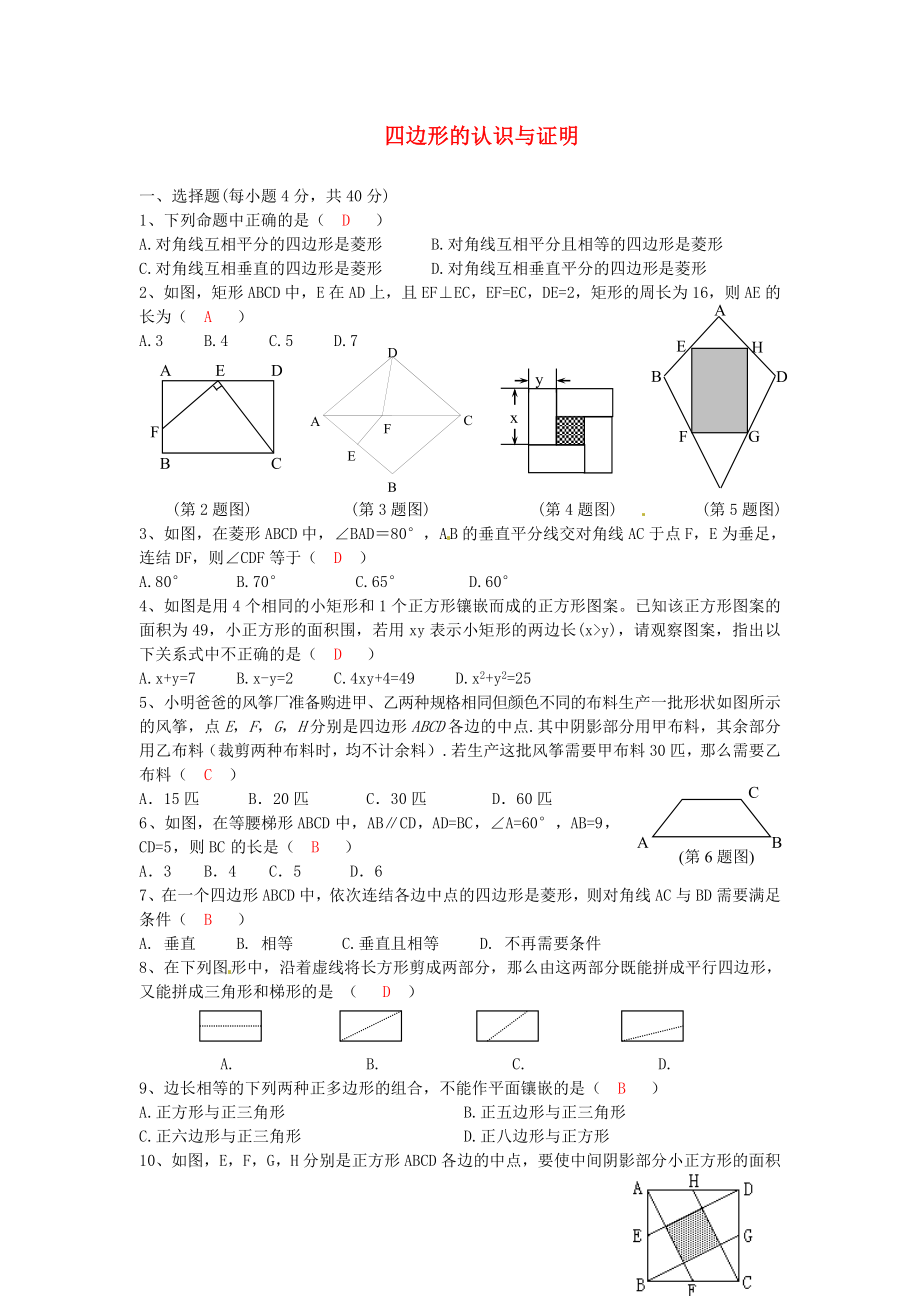
1、四邊形的認(rèn)識(shí)與證明 一、選擇題(每小題4分，共40分) 1、下列命題中正確的是（ D ） A.對(duì)角線互相平分的四邊形是菱形 B.對(duì)角線互相平分且相等的四邊形是菱形 C.對(duì)角線互相垂直的四邊形是菱形 D.對(duì)角線互相垂直平分的四邊形是菱形 A E H D F G B C 2、如圖，矩形ABCD中，E在AD上，且EF⊥EC，EF=EC，DE=2，矩形的周長(zhǎng)為16，則AE的長(zhǎng)為（ A ） F E D C B A A.3 B.4 C.5 D.7 x y B C D A F E

2、 (第2題圖) (第3題圖) (第4題圖) (第5題圖) 3、如圖，在菱形ABCD中，∠BAD＝80°，AB的垂直平分線交對(duì)角線AC于點(diǎn)F，E為垂足，連結(jié)DF，則∠CDF等于（ D ） A.80° B.70° C.65° D.60° 4、如圖是用4個(gè)相同的小矩形和1個(gè)正方形鑲嵌而成的正方形圖案。已知該正方形圖案的面積為49，小正方形的面積圍，若用xy表示小矩形的兩邊長(zhǎng)(x>y)，請(qǐng)觀察圖案，指出以下關(guān)系式中不正確的是（ D ） A.x+y=

3、7 B.x-y=2 C.4xy+4=49 D.x2+y2=25 A B C D (第6題圖) 5、小明爸爸的風(fēng)箏廠準(zhǔn)備購(gòu)進(jìn)甲、乙兩種規(guī)格相同但顏色不同的布料生產(chǎn)一批形狀如圖所示的風(fēng)箏，點(diǎn)E，F(xiàn)，G，H分別是四邊形ABCD各邊的中點(diǎn).其中陰影部分用甲布料，其余部分用乙布料（裁剪兩種布料時(shí)，均不計(jì)余料）.若生產(chǎn)這批風(fēng)箏需要甲布料30匹，那么需要乙布料（ C ） A．15匹 B．20匹 C．30匹 D．60匹 6、如圖，在等腰梯形ABCD中，AB∥CD，AD=BC，∠A=60°，AB=9，CD=5，則BC的長(zhǎng)是（ B

4、 ） A．3 B．4 C．5 D．6 7、在一個(gè)四邊形ABCD中，依次連結(jié)各邊中點(diǎn)的四邊形是菱形，則對(duì)角線AC與BD需要滿足條件（ B ） A. 垂直 B. 相等 C.垂直且相等 D. 不再需要條件 8、在下列圖形中，沿著虛線將長(zhǎng)方形剪成兩部分，那么由這兩部分既能拼成平行四邊形，又能拼成三角形和梯形的是 （ D ） A. B. C. D. 9、邊長(zhǎng)相等的下列兩種正多邊形的組合，不能作平面鑲嵌的是（ B ） A.正方

5、形與正三角形　　　　　　　　　　　B.正五邊形與正三角形 C.正六邊形與正三角形　　　　　　　　　　D.正八邊形與正方形 10、如圖，E，F(xiàn)，G，H分別是正方形ABCD各邊的中點(diǎn)，要使中間陰影部分小正方形的面積是5，那么大正方形的邊長(zhǎng)應(yīng)該是（ C ） A. B. C.5 D. 二、填空題(每小題4分，共20分) C F D A B E B C A D F E A D C B F E 11、在□ABCD中，AB=4cm，AD=7cm，∠ABC的平分線交AD于點(diǎn)E，交CD的延長(zhǎng)線于點(diǎn)F，則DF= 3 cm.

6、 (第11題圖) (第12題圖) (第13題圖) 12、如圖，一張矩形紙片，要折疊出一個(gè)最大的正方形.小明把矩形的一個(gè)角沿折痕AE翻折上去，使AB和AD邊上的AF重合，則四邊形ABEF就是一個(gè)最大的正方形.他的判定方法是____有一組鄰邊相等的矩形是正方形等________________________________. 13、如圖，在長(zhǎng)方形ABCD中，AB=3，BC=2，E為BC的中點(diǎn)，F(xiàn)在AB上，且BF=2AF，則四邊形AFEC的面積為 2 . 14、將一塊正六邊形硬紙片(如圖1)，

7、做成一個(gè)底面仍為正六邊形且高相等的無(wú)蓋紙盒(側(cè)面均垂直于底面，如圖2)，需在每一個(gè)頂點(diǎn)處剪去一個(gè)四邊形，例如圖1中的四邊形AGA/H，那么∠GA/H的大小是 60 度。 圖1 圖2 (第11題圖) (第12題圖) 15、如圖，是一種“羊頭”形圖案，其作法是：從正方形①開(kāi)始，以它的一邊為斜邊，向外作等腰直角三角形，然后再以其直角邊為邊，分別向外作正方形②和②，…，依此類推，若正方形①的邊長(zhǎng)為64cm，則正方形⑦的邊長(zhǎng)為 8 cm. 三、(每小題8分，共16分) D C B A

8、 E F 16、已知：如圖，四邊形AEFD和四邊形EBCF都是平行四邊形. 求證：△ABE≌△DCF. 證明略 A B C E F D 17、如圖，在正方形ABCD的邊BC的延長(zhǎng)線上取一點(diǎn)E，使CE=CA，AE與CD交于F點(diǎn)．求∠AFC的度數(shù)． 112.5° 四、(每小題9分，共18分) 18、用剪刀將形狀如圖1所示的矩形紙片ABCD沿著直線CM剪成兩部分,其中M為AD的中點(diǎn).用這兩部分紙片可以拼成一些新圖形,例如圖2中的Rt△BCE就是拼成的一個(gè)圖形. E B A C B A M C D M 圖3 圖

9、4 圖1 圖2 (1)用這兩部分紙片除了可以拼成圖2中的Rt△BCE外,還可以拼成一些四邊形.請(qǐng)你試一試,把拼好的四邊形分別畫(huà)在圖3、圖4的虛框內(nèi). (2)若利用這兩部分紙片拼成的Rt△BCE是等腰直角三角形，設(shè)原矩形紙片的周長(zhǎng)為12厘米，試求出原矩形紙片的面積. B A C E M 圖3 C B A M 圖4 E （1） （2）由題可知AB＝CD＝AE，又BC＝BE＝AB＋AE ∴BC＝2AB 由題意知　AB+BC=6 ∴AB=2，BC=4 ∴S矩形=AB×BC=8 答：原矩形紙片的面積為8c

10、m2. 19、已知：如圖，四邊形ABCD中，AB=DC，AC=BD，AD≠BC. A B C D 求證：四邊形ABCD是等腰梯形. 證明略 五、(每小題10分，共20分) 20、已知：如圖，D是△ABC的邊AB上一點(diǎn)，CN∥AB，DN交AC于點(diǎn)M，MA=MC. 求證：CD=AN. 證明略 21、如圖，在直角梯形ABCD中，AD∥BC，CD⊥BC，E為BC邊上的點(diǎn)。將直角梯形沿對(duì)角線BD折疊，使△ABD與△EBD重合(如圖中陰影部分)。若∠A=130°，AB=4cm，求梯形ABCD的高CD的長(zhǎng)(結(jié)果精確到0.1cm). 略

11、 六、(本題12分) 22、如圖，在△ABC中，∠ACB＝90°，BC的垂直平分線DE交BC于D，交AB于E，F(xiàn)在DE上，并且AF＝CE． （1）求證：四邊形ACEF是平行四邊形； （2）當(dāng)∠B的大小滿足什么條件時(shí)，四邊形ACEF是菱形？請(qǐng)回答并證明你的結(jié)論； （3）四邊形ACEF有可能是正方形嗎？為什么？ (1)證明略 (2)當(dāng)∠B=30°時(shí)，四邊形CEF是菱形.證明略 (3)四邊形ACEF不可能是正方形. 七、(本題12分) 23、如圖，四邊形ABCD中，點(diǎn)E在邊CD上，連結(jié)AE、BE.給出下列五個(gè)關(guān)系式：①AD∥BC；②DE＝CE；③∠1＝∠2

12、；④∠3＝∠4；⑤AD＋BC＝AB.將其中的三個(gè)關(guān)系式作為題設(shè)，另外兩個(gè)作為結(jié)論，構(gòu)成一個(gè)命題. (1)用序號(hào)寫(xiě)出一個(gè)真命題（書(shū)寫(xiě)形式如：如果×××，那么××）.并給出證明(6分) (2)用序號(hào)再寫(xiě)出三個(gè)真命題(不要求證明)(6分) A B C D E 2 3 4 1 (3)真命題不止以上四個(gè)，想一想，你還能多寫(xiě)出幾個(gè)真命題(每多寫(xiě)出一個(gè)真命題就給你加1分，最多加2分). (1)如果①②③，那么④⑤ 證明略 (2)如果①②④，那么③⑤；如果①③④，那么②⑤；如果①③⑤，那么②④ (3)如果(1)(2)中四個(gè)命題含假命題(“如果

13、②③④，那么①⑤”)，則不加分；若(3)中含假命題，也不加分. A B C D E F G 八、(本題滿分12分) 24、如圖，在正方形ABCD中，以對(duì)角線AC為一邊作一等邊△ACE，連結(jié)ED并延長(zhǎng)交AC于點(diǎn)F. (1)求證：EF⊥AC； (2)延長(zhǎng)AD交CE于點(diǎn)G，試確定線段DG和線段DE的數(shù)量關(guān)系. (1)證明：由已知,得∴△AED≌△CED . ∴∠AED＝∠CED . 又∵△AEC為等邊三角形,∴EF⊥AC . （2）過(guò)G作GM⊥EF，垂足為M. 由已知和(1) ，得∠AED＝∠CED＝30o，∠EAD＝150 . ∴∠EDG＝45o . ∴MD＝GM . 設(shè)GM＝x,則DG＝.在Rt△MEG中，EG＝2MG＝2x , ∴EM＝. ∴ED＝+x＝()x . ∴.即DE＝DG (或).