《人教版九下數(shù)學(xué) 第二十七章 方法技巧專題一 方法技巧3 巧證比例式或等積式（三）等比代換法（找中間比）》由會員分享，可在線閱讀，更多相關(guān)《人教版九下數(shù)學(xué) 第二十七章 方法技巧專題一 方法技巧3 巧證比例式或等積式（三）等比代換法（找中間比）（4頁珍藏版）》請在裝配圖網(wǎng)上搜索。
1、
人教版九下數(shù)學(xué) 第二十七章 方法技巧專題一 方法技巧3 巧證比例式或等積式（三）等比代換法（找中間比）
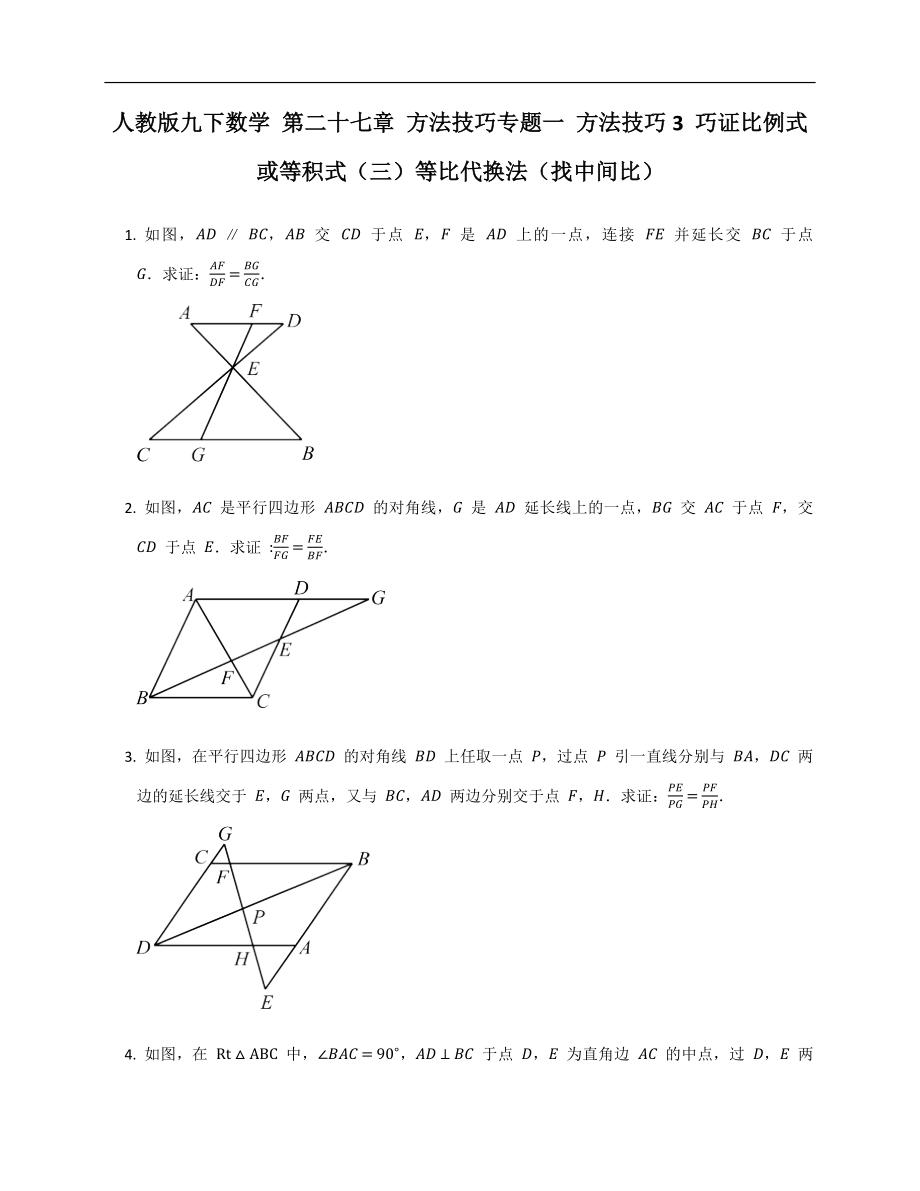
1. 如圖，AD∥BC，AB 交 CD 于點(diǎn) E，F(xiàn) 是 AD 上的一點(diǎn)，連接 FE 并延長交 BC 于點(diǎn) G．求證：AFDF=BGCG．
2. 如圖，AC 是平行四邊形 ABCD 的對角線，G 是 AD 延長線上的一點(diǎn)，BG 交 AC 于點(diǎn) F，交 CD 于點(diǎn) E．求證 :BFFG=FEBF．
3. 如圖，在平行四邊形 ABCD 的對角線 BD 上任取一點(diǎn) P，過點(diǎn) P 引一直線分別與 BA，DC 兩邊的延長線交于 E，G 兩點(diǎn)，又與 BC，AD 兩邊分別
2、交于點(diǎn) F，H．求證：PEPG=PFPH．
4. 如圖，在 Rt△ABC 中，∠BAC=90°，AD⊥BC 于點(diǎn) D，E 為直角邊 AC 的中點(diǎn)，過 D，E 兩點(diǎn)作直線交 AB 的延長線于點(diǎn) F，求證：ABAC=DFAF．
答案
1. 【答案】證 △AFE∽△BGE 得 AFBG=EFEG，
證 △DFE∽△CGE 得 DFCG=EFEG，
∴AFBG=DFCG，即 AFDF=BGCG．
注：本題的中間比是 EFEG．
2. 【答案】 ∵AB∥CD，AD∥BC，
∴△ABF∽△CEF，△AGF∽△CBF，
∴BFEF=AFFC，AFFC=FGBF，
3、
∴BFEF=FGBF，即 BFFG=FEBF．
3. 【答案】 DG∥BE，PEPG=PBPD，BF∥DH，PFPH=PBPD，
∴PEPG=PFPH．
注：本題的中間比是 PBPD．
4. 【答案】 ∵∠BAC=90°，AD⊥BC，
∴∠BAC=∠ADB=90°，
又 ∵∠ABC=∠ABD，
∴△CBA∽△ABD，
∴∠C=∠FAD，ABAC=BDAD，
又 ∵E 為 AC 的中點(diǎn)，AD⊥BC，
∴ED=EC=12AC，
∴∠C=∠EDC，
又 ∵∠EDC=∠FDB，
∴∠FAD=∠FDB，
∵∠F=∠F，
∴△DBF∽△ADF，
∴BDAD=DFAF，
∴ABAC=DFAF．
注：本題的中間比是 BDAD．
人教版九下數(shù)學(xué) 第二十七章 方法技巧專題一 方法技巧3 巧證比例式或等積式（三）等比代換法（找中間比）
