《福建省永安市第七中學(xué)八年級(jí)數(shù)學(xué)《等腰三角形的性質(zhì)》.ppt》由會(huì)員分享�����,可在線閱讀�����,更多相關(guān)《福建省永安市第七中學(xué)八年級(jí)數(shù)學(xué)《等腰三角形的性質(zhì)》.ppt(12頁(yè)珍藏版)》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索��。
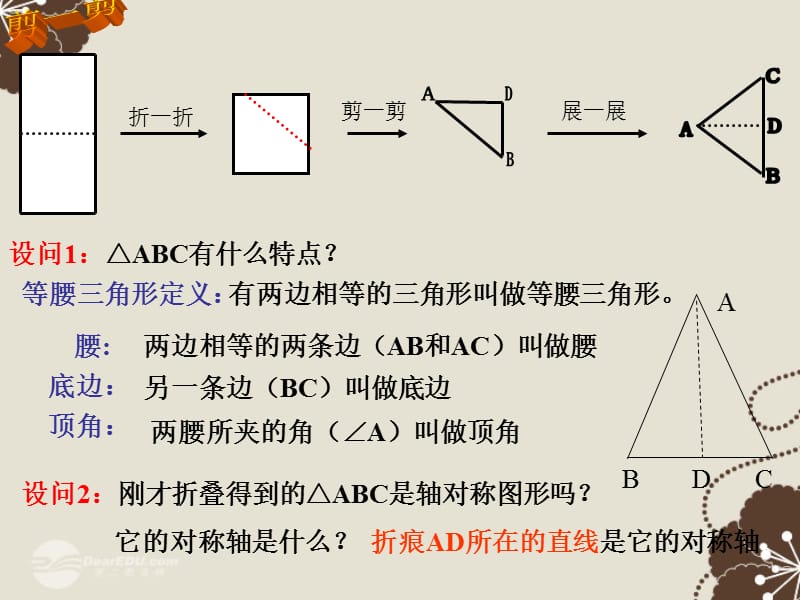
1�����、設(shè)問1:ABC有什么特點(diǎn)��?,等腰三角形定義:,有兩邊相等的三角形叫做等腰三角形��。,兩邊相等的兩條邊(AB和AC)叫做腰,另一條邊(BC)叫做底邊,兩腰所夾的角(A)叫做頂角,剪一剪,設(shè)問2:剛才折疊得到的ABC是軸對(duì)稱圖形嗎�����? 它的對(duì)稱軸是什么�����?,折痕AD所在的直線是它的對(duì)稱軸,設(shè)問3:由折疊,你能發(fā)現(xiàn)等腰三角形有什么性質(zhì)���?,, B = C BD = CD BAD=CDA ADC= ADB=900 AB=AC,等腰三角形性質(zhì): 性質(zhì)1 等腰三角形的兩個(gè)底角相等�。,性質(zhì)2 等腰三角形的頂角平分線���、底邊上的中線�、底 邊 上的高互相重合���。,(可簡(jiǎn)記為“三線合一”
2��、),(簡(jiǎn)寫成“等邊對(duì)等角”)����;, 兩個(gè)底角相等, AD為底邊BC上的中線, AD為頂角BAC的平分線, AD為底邊BC上的高, 等腰三角形的兩腰相等,設(shè)問4:你能用所學(xué)的知識(shí)證明等腰三角形的性質(zhì)(1)嗎�?,已知:ABC中,AB=AC���。求證:B=C。,證明:作底邊BC的中線AD. 在ABD 和ACD中��,, ABD ACD(SSS). B=C.,受性質(zhì)1證明的啟發(fā)�,你能證明性質(zhì)2嗎����?,問:輔助線還有另外作法嗎��?,如何用幾何語(yǔ)言表示性質(zhì)1與性質(zhì)2�����?,性質(zhì)2 等腰三角形的頂角平分線�����、底邊上的中線��、底 邊上的高互相重合��。,等腰三角形性質(zhì): 性質(zhì)1 等腰三角形的兩個(gè)底角相等�。,性質(zhì)2 等腰三角形的頂角平分
3、線���、底邊上的中線���、底 邊 上的高互相重合。,(可簡(jiǎn)記為“三線合一”),(簡(jiǎn)寫成“等邊對(duì)等角”)����;,幾何語(yǔ)言表示:,AB=AC, B=C,(等腰三角形的兩個(gè)底角相等),AB=AC,, BAD=CAD,BD=CD, ADBC,(三線合一),等邊對(duì)等角,在等腰三角形中, (1)已知頂角為70����,其余兩個(gè)角分別為�����。 (2)已知底角為70����,其余兩個(gè)角分別為。,(3)已知一個(gè)角為70, 其余兩個(gè)角分別為 (4)已知一個(gè)角為100����,其余兩個(gè)角分別為,(5)已知等腰三角形的兩邊長(zhǎng)分別是4和6,則它的周長(zhǎng)是( ) A��、14 B����、15 C、16 D�、14或16,55���,55,70�����,40,例1���、在ABC中�����,AB
4���、=AC,點(diǎn)D在AC上�����,且BD=BC=AD�����。 (1)圖中共有幾個(gè)等腰三角形�?分別寫出它們的頂角和底角。 (2)你能求出ABC各角的度數(shù)嗎�?,練習(xí): 已知:如圖��,房屋的頂角BAC=100 , 過(guò)屋頂A的立柱AD BC , 屋椽AB=AC. 求頂架上B�、C�、BAD、 CAD的度數(shù).,BAD=CAD=50,,A,B,C,D,已知:如圖����,AB=BC=CD=ED=EF.,,E,,,,,F,M,N,A=15,試求 FEM的度數(shù)��?,已知:點(diǎn)D�����、E在ABC中, AB=AC,AD=AE. 求證:BD=CE��。,A,B,C,D,,,,E,猜想一下�,等腰三角形底邊中點(diǎn)到兩腰的距離相等嗎?,(高DE=DF����?),(中線DE=DF?),(角平線DE=DF�?),1、研究有關(guān)等腰三角形的問題, 頂角平分線�����、底邊中線���,底邊的 高是常用的輔助線;,2�����、熟練求解等腰三角形的頂 角��、底角的度數(shù)��;,共同特點(diǎn),
 福建省永安市第七中學(xué)八年級(jí)數(shù)學(xué)《等腰三角形的性質(zhì)》.ppt
福建省永安市第七中學(xué)八年級(jí)數(shù)學(xué)《等腰三角形的性質(zhì)》.ppt