《2015屆高考數(shù)學(xué)總復(fù)習(xí) 基礎(chǔ)知識(shí)名師講義 第四章 第一節(jié)向量與向量的線性運(yùn)算 文》由會(huì)員分享���,可在線閱讀,更多相關(guān)《2015屆高考數(shù)學(xué)總復(fù)習(xí) 基礎(chǔ)知識(shí)名師講義 第四章 第一節(jié)向量與向量的線性運(yùn)算 文(12頁珍藏版)》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索���。
1���、
【金版學(xué)案】2015屆高考數(shù)學(xué)總復(fù)習(xí) 基礎(chǔ)知識(shí)名師講義 第四章 第一節(jié)向量與向量的線性運(yùn)算 文
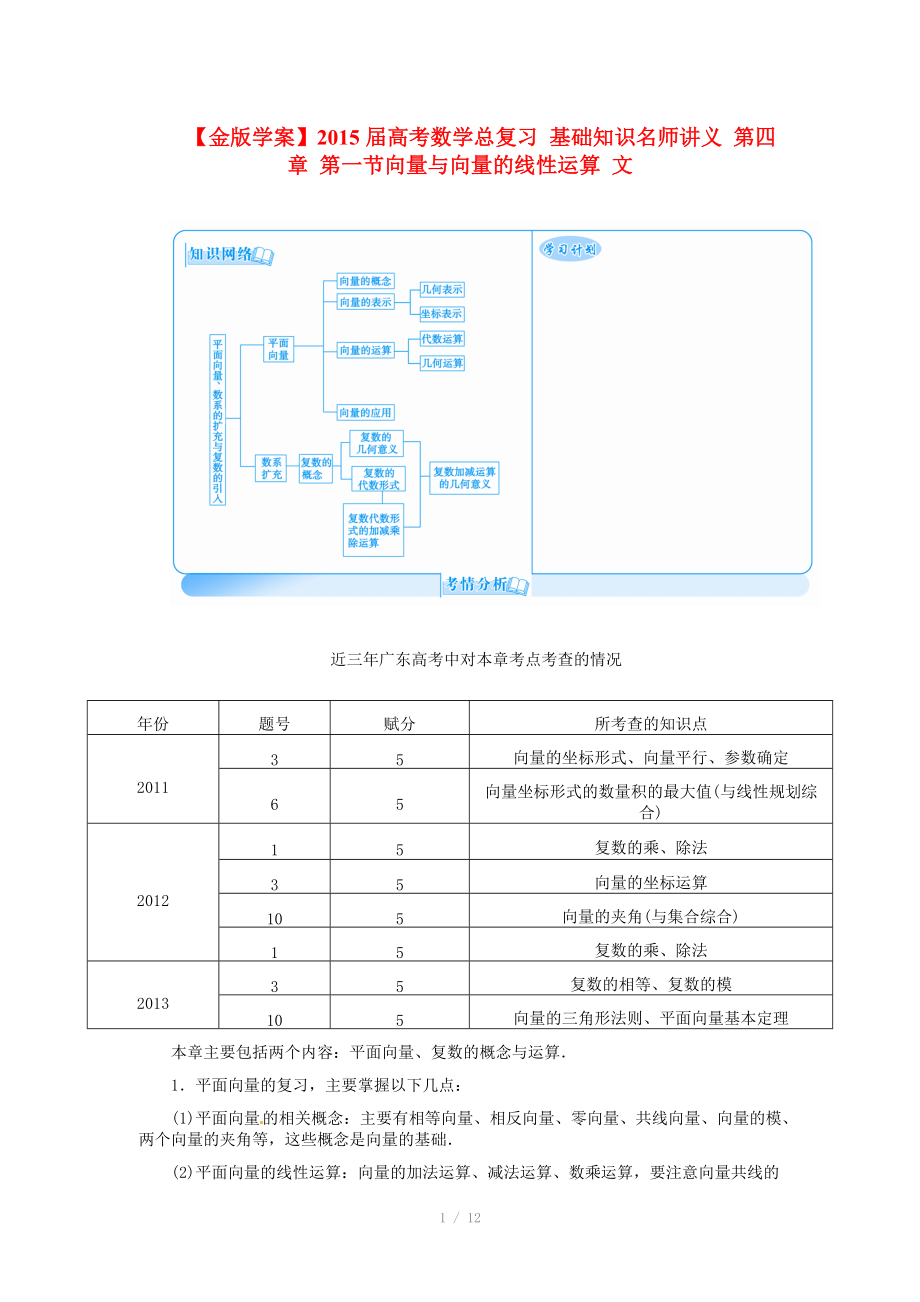
近三年廣東高考中對(duì)本章考點(diǎn)考查的情況
年份
題號(hào)
賦分
所考查的知識(shí)點(diǎn)
2011
3
5
向量的坐標(biāo)形式、向量平行���、參數(shù)確定
6
5
向量坐標(biāo)形式的數(shù)量積的最大值(與線性規(guī)劃綜合)
2012
1
5
復(fù)數(shù)的乘���、除法
3
5
向量的坐標(biāo)運(yùn)算
10
5
向量的夾角(與集合綜合)
1
5
復(fù)數(shù)的乘���、除法
2013
3
5
復(fù)數(shù)的相等、復(fù)數(shù)的模
10
5
向量的三角形法則���、平面向量基本定理
本章主要包括兩個(gè)內(nèi)容:平面向量���、
2���、復(fù)數(shù)的概念與運(yùn)算.
1.平面向量的復(fù)習(xí),主要掌握以下幾點(diǎn):
(1)平面向量的相關(guān)概念:主要有相等向量���、相反向量���、零向量、共線向量���、向量的模���、兩個(gè)向量的夾角等,這些概念是向量的基礎(chǔ).
(2)平面向量的線性運(yùn)算:向量的加法運(yùn)算���、減法運(yùn)算���、數(shù)乘運(yùn)算,要注意向量共線的充要條件的應(yīng)用.
2 / 12
(3)平面向量的基本定理:這個(gè)定理是平面向量的核心���,有了這個(gè)定理���,實(shí)現(xiàn)了平面向量的坐標(biāo)化運(yùn)算.
(4)平面向量的數(shù)量積是平面向量的主要公式���,利用這個(gè)公式,可以求出兩個(gè)向量的夾角���,判斷兩個(gè)向量的垂直與平行.
2.復(fù)數(shù)的復(fù)習(xí)���,主要掌握以下幾點(diǎn):
(1)復(fù)數(shù)的概念:復(fù)數(shù)的定義,復(fù)數(shù)的實(shí)部���、虛部
3、���,復(fù)數(shù)的相等���,共軛復(fù)數(shù),復(fù)數(shù)的模.
(2)復(fù)數(shù)的運(yùn)算:復(fù)數(shù)的四則運(yùn)算中���,除法運(yùn)算是將分母實(shí)數(shù)化.
(3)復(fù)數(shù)加減運(yùn)算的幾何意義.
預(yù)測高考對(duì)平面向量的考查仍以小題考查重要知識(shí)點(diǎn)���,以中、低難度為主;在解答題中���,會(huì)與三角函數(shù)���、解三角形、解析幾何等結(jié)合綜合考查向量的應(yīng)用.對(duì)復(fù)數(shù)的考查���,仍會(huì)以小題考查復(fù)數(shù)的概念與四則運(yùn)算���,以容易題為主.
1.復(fù)習(xí)平面向量內(nèi)容時(shí)要注意:
(1)向量具有大小和方向兩個(gè)要素.用有向線段表示向量時(shí),與有向線段起點(diǎn)的位置沒有關(guān)系���,同向且等長的有向線段都表示同一向量.
(2)共線向量和平面向量的兩條基本定理���,揭示了共線向量和平面向量的基本結(jié)構(gòu),它們是進(jìn)一步研究向量
4���、的基礎(chǔ).
(3)向量的加���、減、數(shù)乘是向量的線性運(yùn)算���,其結(jié)果仍是向量.向量的數(shù)量積結(jié)果是一個(gè)實(shí)數(shù).向量的數(shù)量積���,可以計(jì)算向量的長度���、平面內(nèi)兩點(diǎn)間的距離、兩個(gè)向量的夾角���,判斷相應(yīng)的兩條直線是否垂直.
(4)向量的運(yùn)算與實(shí)數(shù)的運(yùn)算有異同點(diǎn)���,學(xué)習(xí)時(shí)要注意這一點(diǎn),如數(shù)量積不滿足結(jié)合律.
(5)要注意向量在幾何���、三角、物理學(xué)中的應(yīng)用.
(6)平面向量的數(shù)量積及坐標(biāo)運(yùn)算是高考的重點(diǎn)���,復(fù)習(xí)中要注意培養(yǎng)準(zhǔn)確的運(yùn)算能力和靈活運(yùn)用知識(shí)的能力.
2.對(duì)于復(fù)數(shù)���,《課標(biāo)》及《考綱》的要求有以下三點(diǎn):理解復(fù)數(shù)的基本概念,理解復(fù)數(shù)相等的充要條件���,會(huì)進(jìn)行復(fù)數(shù)代數(shù)形式的四則運(yùn)算.所以在復(fù)習(xí)中應(yīng)掌握好以下幾個(gè)方面:
(
5���、1)掌握好復(fù)數(shù)的基本概念和復(fù)數(shù)表示實(shí)數(shù)���、虛數(shù)、純虛數(shù)的充要條件.
(2)熟練掌握復(fù)數(shù)代數(shù)形式的加���、減���、乘、除運(yùn)算法則.在運(yùn)算過程中要注意復(fù)數(shù)運(yùn)算法則與實(shí)數(shù)運(yùn)算法則的區(qū)別.
第一節(jié) 向量與向量的線性運(yùn)算
1.平面向量的實(shí)際背景及基本概念.
(1)了解向量的實(shí)際背景.
(2)理解平面向量的概念���,理解兩個(gè)向量相等的含義.
(3)理解向量的幾何表示.
2.向量的線性運(yùn)算.
(1)掌握向量加法���、減法的運(yùn)算,并理解其幾何意義.
(2)掌握向量數(shù)乘的運(yùn)算及其意義���,理解兩個(gè)向量共線的含義.
(3)了解向量線性運(yùn)算的性質(zhì)及其幾何意義.
知識(shí)梳理
一���、向
6、量的有關(guān)概念
1.平面向量.
平面內(nèi)既有大小又有方向的量叫做向量.
向量一般用a���,b���,c���,……來表示,或用有向線段的起點(diǎn)與終點(diǎn)的大寫字母表示���,如.向量的大小即向量的模(長度)���,記作||,向量a的大小���,記作|a|.
向量不能比較大小���,但向量的模可以比較大?��。?
2.零向量.
長度為零的向量叫做零向量,記為0���,其方向是任意的���,0與任意向量平行.零向量a=0?|a|=0.
由于0的方向是任意的���,且規(guī)定0平行于任何向量,故在有關(guān)向量平行(共線)的問題中務(wù)必看清楚是否有“非零向量”這個(gè)條件(注意“0”與“0”的區(qū)別).
3.單位向量.
模為1個(gè)單位長度的向量叫做單位向量.向量a0為單位向
7���、量?|a0|=1.
4.平行向量(共線向量).
方向相同或相反的非零向量叫做平行向量���,記作a∥b.由于向量可以進(jìn)行任意的平移(即自由向量),平行向量總可以平移到同一直線上���,故平行向量也稱為共線向量.
數(shù)學(xué)中研究的向量是自由向量���,只有大小、方向兩個(gè)要素���,起點(diǎn)可以任意選取���,這里必須區(qū)分清楚共線向量中的“共線”與幾何中的“共線”的含義,要理解好平行向量中的“平行”與幾何中的“平行”是不一樣的.
5.相等向量.
長度相等且方向相同的向量叫做相等向量.相等向量經(jīng)過平移后總可以重合���,記為a=b.
二���、向量的運(yùn)算
1.向量的加法.
求兩個(gè)向量和的運(yùn)算叫做向量的加法.
設(shè)=a���,=b
8、���,則a+b=+=.
規(guī)定:(1)0+a=a+0=a���;
(2)向量加法滿足交換律與結(jié)合律.
向量加法的三角形法則可推廣至多個(gè)向量相加:+++…++=,但這時(shí)必須“首尾相連”.
2.向量的減法.
(1)相反向量:與a長度相等���、方向相反的向量叫做a的相反向量���,記作-a.零向量的相反向量仍是零向量.
關(guān)于相反向量有:①-(-a)=a;②a+(-a)=(-a)+a=0���;③若a���,b互為相反向量,則a=-b���,b=-a���,a+b=0.
(2)向量的減法:向量a加上b的相反向量叫做a與b的差,記作a-b=a+(-b).求兩個(gè)向量差的運(yùn)算叫做向量的減法.
(3)作圖法:a-b可以表示為從b的終點(diǎn)指向
9���、a的終點(diǎn)的向量(a���,b有共同起點(diǎn)).
3.向量加、減法的“三角形法則”與“平行四邊形法則”.
(1)用平行四邊形法則時(shí)���,兩個(gè)已知向量是要共始點(diǎn)的���,和向量是始點(diǎn)與已知向量的始點(diǎn)重合的那條對(duì)角線,而差向量是另一條對(duì)角線���,方向是從減向量指向被減向量.
(2)三角形法則的特點(diǎn)是“首尾相接”���,由第一個(gè)向量的起點(diǎn)指向最后一個(gè)向量的終點(diǎn)的有向線段就表示這些向量的和,差向量是從減向量的終點(diǎn)指向被減向量的終點(diǎn).
當(dāng)兩個(gè)向量的起點(diǎn)公共時(shí)���,用平行四邊形法則���;當(dāng)兩向量是首尾連接時(shí),用三角形法則.
4.實(shí)數(shù)與向量的積.
(1)實(shí)數(shù)λ與向量a的積是一個(gè)向量���,記作λa���,它的長度與方向規(guī)定如下:
①=���;
②當(dāng)
10、λ>0時(shí)���,λa的方向與a的方向相同���;當(dāng)λ<0時(shí),λa的方向與a的方向相反���;當(dāng)
λ=0時(shí)���,λa=0,方向是任意的.
(2)數(shù)乘向量滿足交換律���、結(jié)合律與分配律.
三���、兩個(gè)向量共線定理
向量b與非零向量a共線?有且只有一個(gè)實(shí)數(shù)λ,使得b=λ a.
基礎(chǔ)自測
1.(2012·惠州調(diào)研)已知向量a,b���,則“a∥b”是“a+b=0”的________條件( )
A.充分不必要 B.必要不充分
C.充要 D.既不充分也不必要
解析:“a∥b”只要求兩向量共線,而“a+b=0”要求反向共線且模相等.故選B.
答案:B
2
11���、.(2013·增城下學(xué)期調(diào)研)設(shè)M是平行四邊形ABCD的對(duì)角線的交點(diǎn)���,O為任意一點(diǎn),則+++=( )
A. B.2 C.3 D.4
解析:在△OAC中���,M為AC中點(diǎn)���,根據(jù)平行四邊形法則,有+=2���,同理有+=2���,所以+++=4.故選D.
答案:D
3.如圖,
e1���,e2為互相垂直的單位向量���,則向量a-b可表示為________________.
解析:如圖所示���,a-b=e1-3e2.
答案:e1-3e2
4.(2013·江蘇南通高三期末考試)在△ABC中,a���,b���,c分別是角A,B���,C所對(duì)的邊���,且3a+4b+
12、5c=0���,則abc=________.
解析:由3a+4b-5c(+)=0.
得3a+4b-5c-5c=0.
即(3a-5c)+(4b-5c)=0.
因?yàn)榕c不共線���,所以3a-5c=0,且4b-5c=0.
所以abc=201512.
答案:201512
1.如圖���,正六邊形ABCDEF中���,++=( )
A.0 B. C. D.
解析:++=++=.故選D.
答案:D
2.(2013·四川卷)如圖���,
在平行四邊形ABCD中,對(duì)角線AC與BD交于點(diǎn)O���,+=λ,則λ=________.
解析:由于
13���、ABCD為平行四邊形���,對(duì)角線AC與BD交于點(diǎn)O,
所以+==2���,所以λ=2.
答案:2
1.(2012·揭陽模擬)已知點(diǎn)O為△ABC外接圓的圓心���,且++=0,則△ABC的內(nèi)角A等于( )
A.30° B.60° C.90° D.120°
解析:由++=0得+=���,由O為△ABC外接圓的圓心���,結(jié)合向量加法的幾何意義知四邊形OACB為菱形���,且∠CAO=60°,從而△ABC的內(nèi)角∠A=30°.故選A.
答案:A
2.(2012·華南師大附中綜合測試)在平行四邊形ABCD中���,E���,F(xiàn)分別是CD和BC的中點(diǎn),若=λ+γ���,其中λ���,γ∈R,則λ+γ=________.
解析:由向量加法的三角形法則得=+=(-)+(-)=(+)-(+)=(+)-(+)=(+)-���,
所以=(+)���,所以λ+γ=+=.
答案:
希望對(duì)大家有所幫助,多謝您的瀏覽���!
 2015屆高考數(shù)學(xué)總復(fù)習(xí) 基礎(chǔ)知識(shí)名師講義 第四章 第一節(jié)向量與向量的線性運(yùn)算 文
2015屆高考數(shù)學(xué)總復(fù)習(xí) 基礎(chǔ)知識(shí)名師講義 第四章 第一節(jié)向量與向量的線性運(yùn)算 文