《高考數(shù)學復習:第三章 :第六節(jié)正弦定理和余弦定理回扣主干知識提升學科素養(yǎng)》由會員分享�,可在線閱讀�,更多相關《高考數(shù)學復習:第三章 :第六節(jié)正弦定理和余弦定理回扣主干知識提升學科素養(yǎng)(4頁珍藏版)》請在裝配圖網(wǎng)上搜索�。
1、△+△2019年數(shù)學高考教學資料△+△
【考綱下載】
掌握正弦定理�����、余弦定理���,并能解決一些簡單的三角形度量問題.
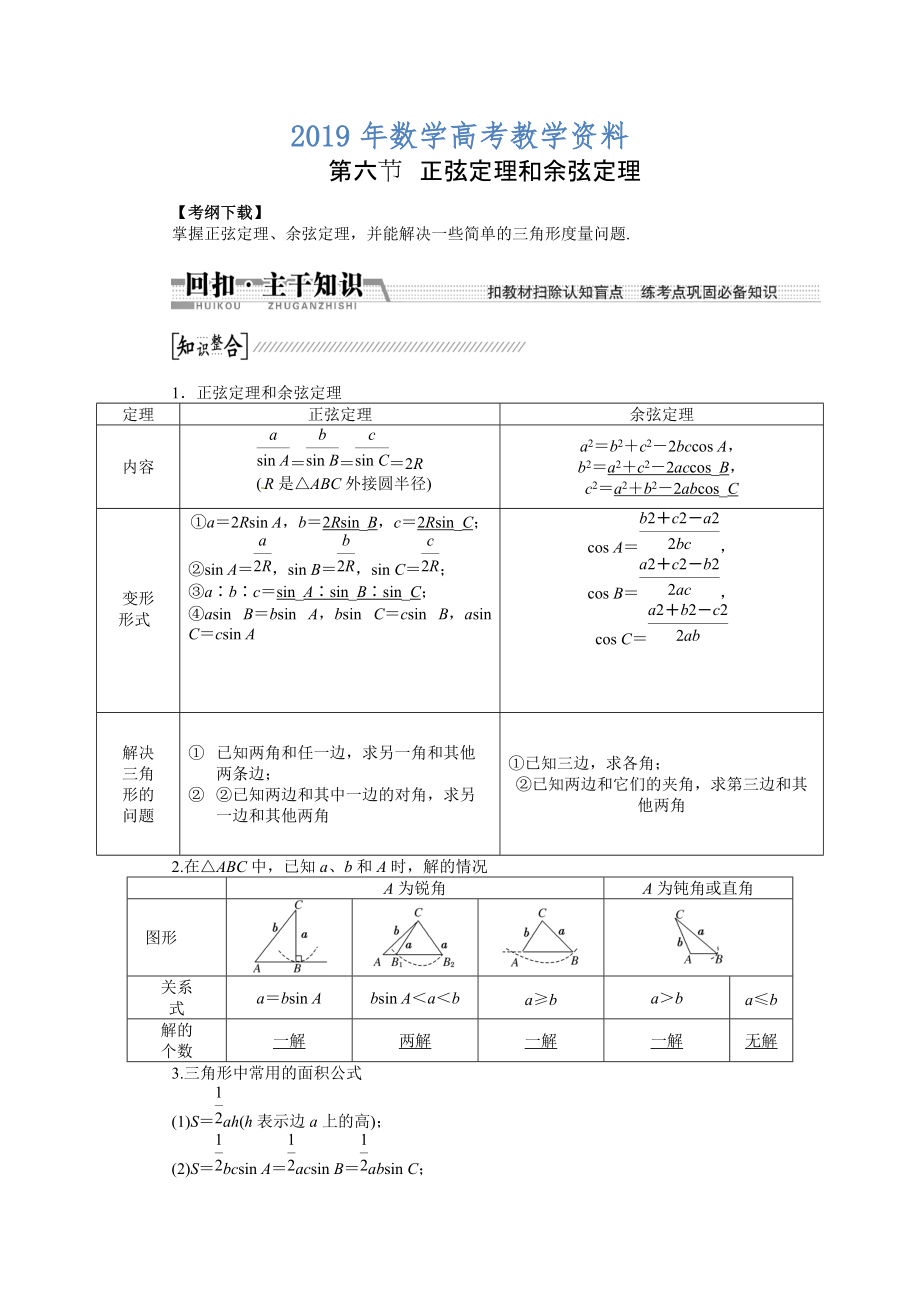
1.正弦定理和余弦定理[來源:]
定理
正弦定理
余弦定理
內(nèi)容
===2R
(R是△ABC外接圓半徑)
a2=b2+c2-2bccos A�,
b2=a2+c2-2accos_B��,
c2=a2+b2-2abcos_C
變形
形式[來源:]
①a=2Rsin A�,b=2Rsin_B,c=2Rsin_C�����;
②sin A=���,sin B=��,sin C=�;
③a∶b∶c=sin_A∶sin_B∶sin_C�����;
④asin B=
2�����、bsin A����,bsin C=csin B,asin C=csin A
cos A=�����,
cos B=,
cos C=
解決
三角
形的
問題
① 已知兩角和任一邊��,求另一角和其他兩條邊��;
② ②已知兩邊和其中一邊的對角����,求另一邊和其他兩角
①已知三邊,求各角���;
②已知兩邊和它們的夾角����,求第三邊和其他兩角
2.在△ABC中�����,已知a�、b和A時,解的情況
A為銳角
A為鈍角或直角
圖形[來源:]
關系
式
a=bsin A
bsin A<a<b
a≥b
a>b
a≤b
解的
個數(shù)
一解
兩解
一解
一解
無解
3.三角形中
3�����、常用的面積公式
(1)S=ah(h表示邊a上的高);
(2)S=bcsin A=acsin B=absin C���;
(3)S=r(a+b+c)(r為△ABC內(nèi)切圓半徑).
1.在三角形ABC中,“A>B”是“sin A>sin B”的什么條件�����?“A>B”是“cos A<cos B”的什么條件��?
提示:“A>B”是“sin A>sin B”的充要條件��,“A>B”是“cos A<cos B”的充要條件.
2.在三角形中��,“a2+b2<c2”是“△ABC為鈍角三角形”的什么條件���?“a2+b2>c2”是“△ABC為銳角三角形”的什么條件�����?
提示:“a2+b2<c2”是“△ABC為鈍角三
4���、角形”的充分不必要條件;“a2+b2>c2”是“△ABC為銳角三角形”的必要不充分條件.
1.(2013·北京高考)在△ABC中�����,a=3,b=5�,sin A=,則sin B=( )
A. B. C. D.1
解析:選B 依題意�,由=,即=����,得sin B=.
2.在△ABC中,若a=2��,c=4�,B=60°,則b等于( )
A.2 B.12 C.2 D.28
解析:選A 由余弦定理得b2=a2+c2-2accos B�,
即b2=4+16-8=12,所以b=2.
3.(2013·湖南高考)在銳
5���、角△ABC中�����,角A�����,B所對的邊長分別為a�,b.若2asin B=b,則角A等于( )
A. B. C. D.
解析:選A 由正弦定理可得����,2asin B=b可化為2sin Asin B=sin B,又sin B≠0�����,所以sin A=�����,又△ABC為銳角三角形�����,得A=.
4.在△ABC中����,a=3���,b=2���,cos C=�,則△ABC的面積為________.
解析:∵cos C=�����,∴sin C=���,
∴S△ABC=absin C=×3×2×=4.
答案:4
5.在△ABC中�����,若a=2����,b+c=7���,cos B=-��,則b
6���、=________.
解析:由余弦定理得b2=4+(7-b)2-2×2×(7-b)×,解得b=4.
答案:4
答題模板(三)
利用正、余弦定理解三角形
[典例] (2013·江西高考)(12分)在△ABC中��,角A���,B����,C所對的邊分別為a�,b,c�����,已知cos C+(cos A-sin A)cos B=0.
(1)求角B的大?�?���;
(2)若a+c=1�����,求b的取值范圍.
[快速規(guī)范審題]
第(1)問
1.審結(jié)論��,明解題方向
觀察所求結(jié)論:求角B的大小轉(zhuǎn)化為求sin B、cos B或tan B的值.
2.審條件����,挖解題信息
7、觀察條件:cos C+(cos A-sin A)cos B=0A+B+C=π,cos [π-(A+B)]+(cos A-sin A)cos B=0����,即sin Asin B-sin Acos B=0.
3.建聯(lián)系,找解題突破口
sin Asin B-sin Acos B=0sin B=cos Btan B=B=.
第(2)問
1.審結(jié)論�,明解題方向
觀察所求結(jié)論:求b的取值范圍b2=a2+c2-2accos B.
2.審條件,挖解題信息
觀察條件:B=���,a+c=1可考慮利用余弦定理建立聯(lián)系.
3.建聯(lián)系��,找解題突破口
b2=a2+c2-2accos B→b2=32+求b2的范圍
8�����、���,進而求得結(jié)論.,
[準確規(guī)范答題]
(1)由已知得
-cos(A+B)+cos Acos B-sin Acos B=0,
即有sin Asin B-sin Acos B=0���,?2分
此處易忽視對sin A≠0�����,cos B≠0的說明����,直接得出tan B=,造成解題步驟不完整因為sin A≠0���,所以sin B-cos B=0�����,
又cos B≠0�����,所以tan B=,?4分
此處易忽視B的范圍����,直接得出B=又0<B<π,所以B=.?6分[來源:]
(2)由余弦定理��,得b2=a2+
c2-2accos B.
因為a+c=1���,cos B=��,
所以b2=32+.
?10分
又0<a<1�,于是有≤b2<1,即≤b<1.?12分
[答題模板速成]
解三角形問題一般可用以下幾步解答:
第一步 邊角互化
利用正弦定理或余弦定理實現(xiàn)邊角互化
第二步 三角變換
三角變換�、化簡、消元��,從而向已知角(或邊)轉(zhuǎn)化
第三步 由值求角
代入求值
第四步 反思回顧
查看關鍵點��,易錯點����,如本題中公式應用是否正確,a的取值范圍是否正確
高考數(shù)學復習精品
高考數(shù)學復習精品
 高考數(shù)學復習:第三章 :第六節(jié)正弦定理和余弦定理回扣主干知識提升學科素養(yǎng)
高考數(shù)學復習:第三章 :第六節(jié)正弦定理和余弦定理回扣主干知識提升學科素養(yǎng)