2020-2021學年人教版 八年級數(shù)學上冊 第十二章 全等三角形暑假提高訓練

《2020-2021學年人教版 八年級數(shù)學上冊 第十二章 全等三角形暑假提高訓練》由會員分享，可在線閱讀，更多相關(guān)《2020-2021學年人教版 八年級數(shù)學上冊 第十二章 全等三角形暑假提高訓練（10頁珍藏版）》請在裝配圖網(wǎng)上搜索。

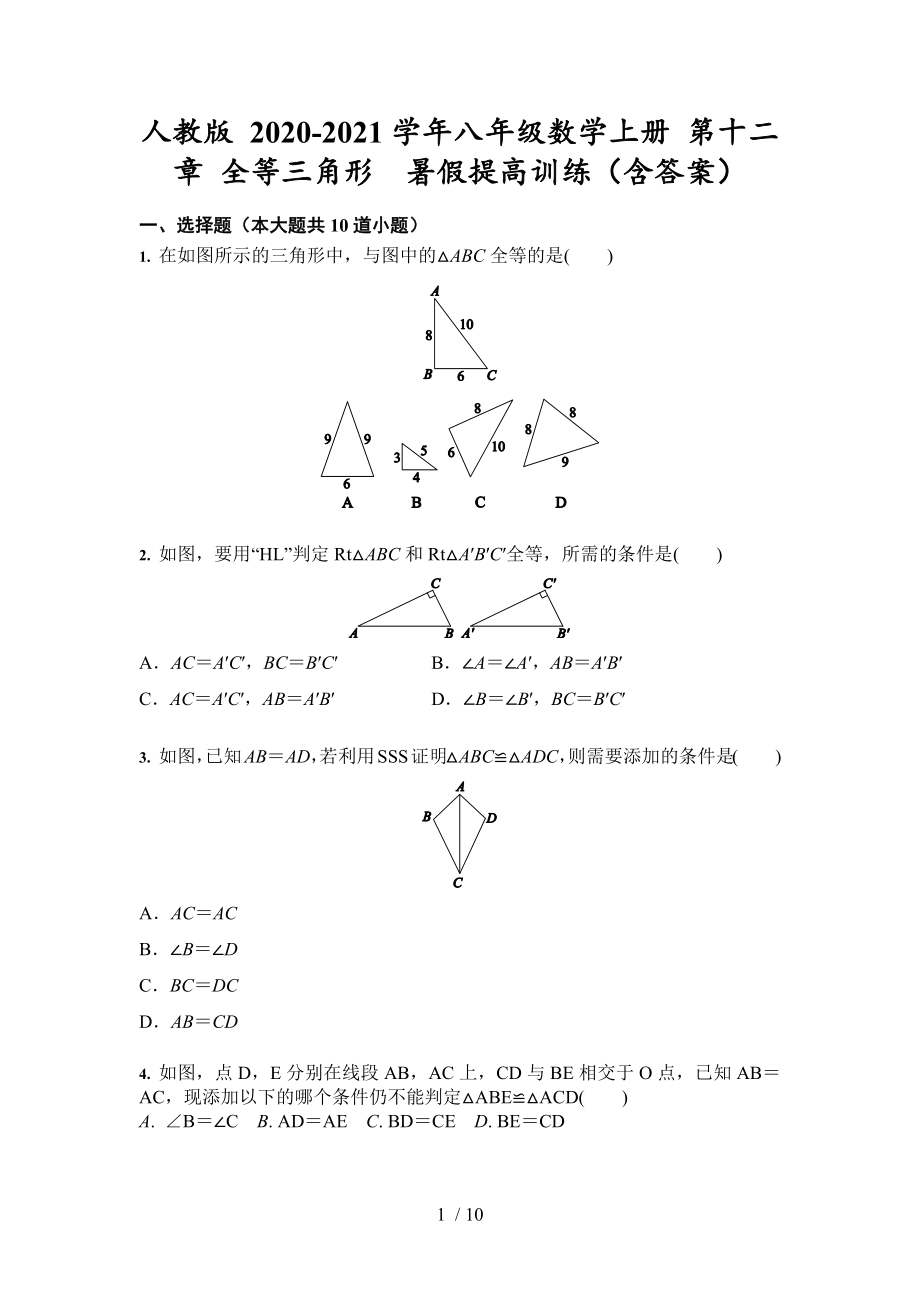
1、人教版 2020-2021學年八年級數(shù)學上冊 第十二章 全等三角形 暑假提高訓練（含答案） 一、選擇題（本大題共10道小題） 1. 在如圖所示的三角形中，與圖中的△ABC全等的是(　　) 2. 如圖，要用“HL”判定Rt△ABC和Rt△A′B′C′全等，所需的條件是(　　) A．AC＝A′C′，BC＝B′C′ B．∠A＝∠A′，AB＝A′B′ C．AC＝A′C′，AB＝A′B′ D．∠B＝∠B′，BC＝B′C′ 3. 如圖，已知AB＝AD，若利用SSS證明△ABC≌△ADC，則需要添加的條件是(　　) A．AC＝AC B．∠B＝∠D C

2、．BC＝DC D．AB＝CD 4. 如圖，點D，E分別在線段AB，AC上，CD與BE相交于O點，已知AB＝AC，現(xiàn)添加以下的哪個條件仍不能判定△ABE≌△ACD(　　) A. ∠B＝∠C B. AD＝AE C. BD＝CE D. BE＝CD 5. 如圖所示，已知AB∥DE，點B，E，C，F(xiàn)在同一直線上，AB＝DE，BE＝CF，∠B＝32°，∠A＝78°，則∠F等于(　　) A．55° B．65° C．60° D．70° 6. 已知△ABC的六個元素，下列甲、乙、丙三個三角形中標出了某些元素，則與△ABC全等的三角形是(　　) A．只

3、有乙　 B．只有丙　 C．甲和乙　 D．乙和丙 7. 如圖，點B，F(xiàn)，C，E在一條直線上，AB∥ED，AC∥FD，那么添加下列一個條件后，仍無法判定△ABC≌△DEF的是(　　) A．AB＝DE B．AC＝DF C．∠A＝∠D D．BF＝EC 8. 如圖，BE⊥AC，CF⊥AB，垂足分別是E，F(xiàn).若BE＝CF，則圖中全等三角形有(　　) A．1對 B．2對 C．3對 D．4對 9. 如圖，若AB＝AC，AD＝AE，∠BAC＝∠DAE，則∠ABD等于(　　) A．∠EAC B．∠ADE C．∠BAD

4、 D．∠ACE 10. 如圖，AB＝AC，AD＝AE，BE＝CD，∠2＝110°，∠BAE＝60°，則下列結(jié)論錯誤的是(　　) A．△ABE≌△ACD B．△ABD≌△ACE C．∠C＝30° D．∠1＝70° 二、填空題（本大題共5道小題） 11. 如圖所示，把△ABC沿直線AC翻折，得到△ADC，則△ABC≌________，AB的對應邊是________，AC的對應邊是________，∠BCA的對應角是________. 　 12. 如圖，在四邊形ABCD中，∠B＝∠D＝90°，AB＝AD，∠BAC＝65°，則∠ACD的度數(shù)為___

5、_____． 13. 如圖，請用符號語言表示“角的平分線上的點到角的兩邊的距離相等”． 條件：____________________________________. 結(jié)論：PC＝PD. 　　　 14. 如圖，PA⊥ON于點A，PB⊥OM于點B，且PA＝PB.若∠MON＝50°，∠OPC＝30°，則∠PCA的大小為________． 15. 要測量河岸相對兩點A，B之間的距離，已知AB垂直于河岸BF，先在BF上取兩點C，D，使CD＝CB，再過點D作BF的垂線段DE，使點A，C，E在一條直線上，如圖，測出DE＝20米，則AB的長是________米．

6、 三、解答題（本大題共4道小題） 16. 如圖，點D，A，E，B在同一直線上，EF＝BC，DF＝AC，DA＝EB.求證：∠F＝∠C. 17. 如圖，A、C、D、B四點共線，且AC＝BD，∠A＝∠B，∠ADE＝∠BCF.求證：DE＝CF. 18. 如圖，已知∠α，∠β(∠α＞∠β)，求作一個角，使它等于∠α－∠β.(不寫作法，保留作圖痕跡，不在原圖上作圖) 19. 楊陽同學沿一段筆直的人行道行走，在由A步行到達B處的過程中，通過隔離帶的空隙O，剛好瀏覽完對面人行道宣傳墻上的社會主義核心價值觀標語．其具體信息匯集如下

7、． 如圖，AB∥OH∥CD，相鄰兩平行線間的距離相等．AC、BD相交于O，OD⊥CD，垂足為D.已知AB＝20米，請根據(jù)上述信息求標語CD的長度． 人教版 2020-2021學年八年級數(shù)學上冊 第十二章 全等三角形 暑假提高訓練 -答案 一、選擇題（本大題共10道小題） 1. 【答案】C 2. 【答案】C　 3. 【答案】C　 4. 【答案】D　【解析】A.當∠B＝∠C時，在△ABE與△ACD中，，∴△ABE≌△ACD(ASA)；B.當AD＝AE時，在△ABE與△ACD中，，

8、∴△ABE≌△ACD(SAS)；C.當BD＝CE時，∵AB＝AC，∴AD＝AE，在△ABE與△ACD中，，∴△ABE≌△ACD(SAS)；D.當BE＝CD時，在△ABE與△ACD中，有AB＝AC，BE＝BD，∠A＝∠A，只滿足兩邊及一對角對應相等的兩個三角形不一定全等．故選D. 5. 【答案】D　[解析] 因為AB∥DE，所以∠B＝∠DEF.由條件BE＝CF知BC＝EF.結(jié)合條件AB＝DE，可由“SAS”判定△ABC≌△DEF，所以∠F＝∠ACB＝180°－(∠A＋∠B)＝180°－(78°＋32°)＝70°. 6. 【答案】D 7. 【答案】C　[解析] 選項A

9、中添加AB＝DE可用“AAS”進行判定，故本選項不符合題意； 選項B中添加AC＝DF可用“AAS”進行判定，故本選項不符合題意； 選項C中添加∠A＝∠D不能判定△ABC≌△DEF，故本選項符合題意； 選項D中添加BF＝EC可得出BC＝EF，然后可用“ASA”進行判定，故本選項不符合題意． 故選C. 8. 【答案】C　[解析] ①∵BE⊥AC，CF⊥AB， ∴∠CFB＝∠BEC＝90°. 在Rt△BCF和Rt△CBE中， ∴Rt△BCF≌Rt△CBE(HL)． ②∵BE⊥AC，CF⊥AB，∴∠AFC＝∠AEB＝90°.在△ABE和△ACF中， ∴△ABE≌△ACF(A

10、AS)． ③設BE與CF相交于點O. ∵BE⊥AC，CF⊥AB， ∴∠OFB＝∠OEC＝90°. ∵△ABE≌△ACF，∴AB＝AC，AE＝AF. ∴BF＝CE. 在△BOF和△COE中， ∴△BOF≌△COE(AAS)． 9. 【答案】D　[解析] ∵∠BAC＝∠DAE，∴∠BAC－∠DAC＝∠DAE－∠DAC，即∠BAD＝∠CAE. 在△ABD和△ACE中， ∴△ABD≌△ACE(SAS)．∴∠ABD＝∠ACE. 10. 【答案】C　[解析] ∵BE＝CD， ∴BE－DE＝CD－DE，即BD＝CE. 在△ABD和△ACE中， ∴△ABD≌△A

11、CE. 由題意易證：△ABE≌△ACD，故A，B正確． 由△ABE≌△ACD可得∠B＝∠C. ∵∠2＝∠BAE＋∠B， ∴∠B＝∠2－∠BAE＝110°－60°＝50°. ∴∠C＝∠B＝50°. 故C錯誤． ∵△ABE≌△ACD(已證)，∴∠1＝∠AED＝180°－∠2＝70°. 故D正確．故選C. 二、填空題（本大題共5道小題） 11. 【答案】△ADC　AD　AC　∠DCA　[解析] △ABC與△ADC重合，則△ABC≌△ADC. 12. 【答案】25° 13. 【答案】∠AOP＝∠BOP，PC⊥OA于點C，PD⊥OB于點D 14.

12、 【答案】55°　[解析] ∵PA⊥ON，PB⊥OM， ∴∠PAO＝∠PBO＝90°. 在Rt△AOP和Rt△BOP中， ∴Rt△AOP≌Rt△BOP(HL)． ∴∠AOP＝∠BOP＝∠MON＝25°. ∴∠PCA＝∠AOP＋∠OPC＝25°＋30°＝55°. 15. 【答案】20 三、解答題（本大題共4道小題） 16. 【答案】 證明：∵DA＝EB， ∴DA＋AE＝EB＋AE，即DE＝AB. 在△DEF和△ABC中， ∴△DEF≌△ABC(SSS)． ∴∠F＝∠C. 17. 【答案】 證明：∵A、C、D、B四點共線，且AC＝BD， ∴AC＋CD＝BD＋CD，即AD＝BC，(2分) 在△ADE和△BCF中， ， ∴△ADE≌△BCF(ASA)，(4分) ∴DE＝CF.(6分) 18. 【答案】 解：如圖，∠AOB即為所求． 19. 【答案】 解：∵AB∥CD，OD⊥CD， ∴OB⊥AB， ∵相鄰兩平行線間的距離相等， ∴OB＝OD.(3分) 在△ABO與△CDO中， ， ∴△ABO≌△CDO(ASA)，(6分) ∴CD＝AB＝20(米)．(7分) 10 / 10