2021-2021學(xué)年七年級數(shù)學(xué)上冊 第4章4.1 幾何圖形例題與講解 （新版）滬科版

《2021-2021學(xué)年七年級數(shù)學(xué)上冊 第4章4.1 幾何圖形例題與講解 （新版）滬科版》由會(huì)員分享，可在線閱讀，更多相關(guān)《2021-2021學(xué)年七年級數(shù)學(xué)上冊 第4章4.1 幾何圖形例題與講解 （新版）滬科版（4頁珍藏版）》請?jiān)谘b配圖網(wǎng)上搜索。

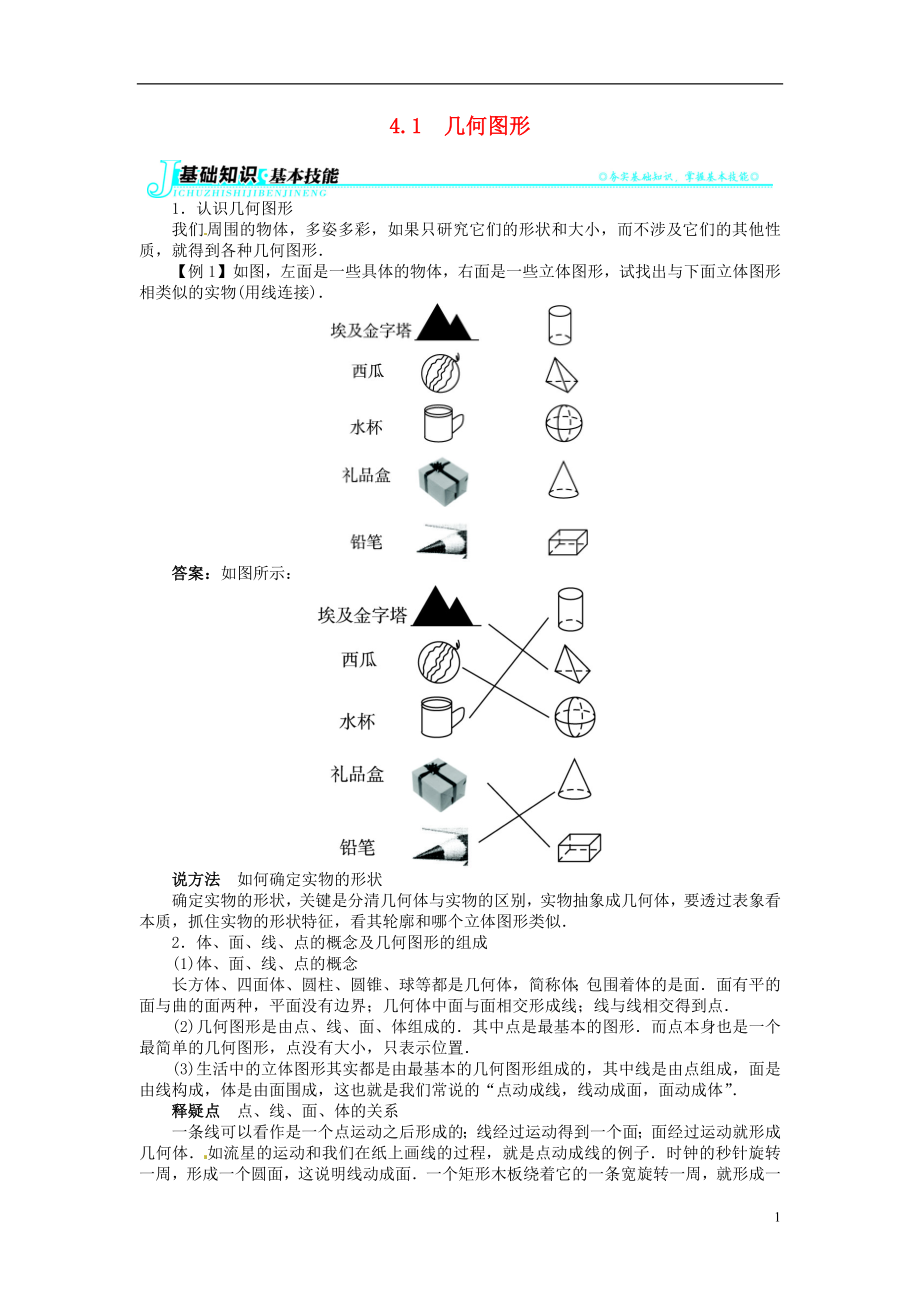
1、 4.1　幾何圖形 1．認(rèn)識幾何圖形 我們周圍的物體，多姿多彩，如果只研究它們的形狀和大小，而不涉及它們的其他性質(zhì)，就得到各種幾何圖形． 【例1】 如圖，左面是一些具體的物體，右面是一些立體圖形，試找出與下面立體圖形相類似的實(shí)物(用線連接)． 答案：如圖所示： 說方法 如何確定實(shí)物的形狀 確定實(shí)物的形狀，關(guān)鍵是分清幾何體與實(shí)物的區(qū)別，實(shí)物抽象成幾何體，要透過表象看本質(zhì)，抓住實(shí)物的形狀特征，看其輪廓和哪個(gè)立體圖形類似． 2．體、面、線、點(diǎn)的概念及幾何圖形的組成 (1)體、面、線、點(diǎn)的概念 長方體、四面體、圓柱、圓錐、球等都是幾何體，簡稱體；包圍著體的是面．面

2、有平的面與曲的面兩種，平面沒有邊界；幾何體中面與面相交形成線；線與線相交得到點(diǎn)． (2)幾何圖形是由點(diǎn)、線、面、體組成的．其中點(diǎn)是最基本的圖形．而點(diǎn)本身也是一個(gè)最簡單的幾何圖形，點(diǎn)沒有大小，只表示位置． (3)生活中的立體圖形其實(shí)都是由最基本的幾何圖形組成的，其中線是由點(diǎn)組成，面是由線構(gòu)成，體是由面圍成，這也就是我們常說的“點(diǎn)動(dòng)成線，線動(dòng)成面，面動(dòng)成體”． 釋疑點(diǎn) 點(diǎn)、線、面、體的關(guān)系 一條線可以看作是一個(gè)點(diǎn)運(yùn)動(dòng)之后形成的；線經(jīng)過運(yùn)動(dòng)得到一個(gè)面；面經(jīng)過運(yùn)動(dòng)就形成幾何體．如流星的運(yùn)動(dòng)和我們在紙上畫線的過程，就是點(diǎn)動(dòng)成線的例子．時(shí)鐘的秒針旋轉(zhuǎn)一周，形成一個(gè)圓面，這說明線動(dòng)成面．一個(gè)矩形木

3、板繞著它的一條寬旋轉(zhuǎn)一周，就形成一個(gè)圓柱，這說明面動(dòng)成體． 【例2－1】 如果我們把流星看作一個(gè)點(diǎn)，那么我們觀察流星移動(dòng)時(shí)，會(huì)看到它劃過一條長弧，這說明了__________，當(dāng)直升機(jī)啟動(dòng)后，隨著螺旋槳轉(zhuǎn)動(dòng)速度的加快，我們會(huì)看到一個(gè)圓面，這說明了__________，把一枚硬幣用左手豎放在桌面上，使右手用力一彈，硬幣會(huì)高速旋轉(zhuǎn)，我們會(huì)看到一個(gè)球，這說明了__________． 答案：點(diǎn)動(dòng)成線　線動(dòng)成面　面動(dòng)成體 說方法 理性認(rèn)識物體的形狀 理解相關(guān)概念，學(xué)會(huì)觀察，對物體形狀的認(rèn)識逐步由感性認(rèn)識上升到理性認(rèn)識． 【例2－2】 將一個(gè)直角三角形繞它的最長邊(斜邊)旋轉(zhuǎn)一周，得到的幾何體

4、是(　　)． 解析： A × 圓柱是由一長方形繞其一邊長旋轉(zhuǎn)而成的 B × 圓錐是由一直角三角形繞其直角邊旋轉(zhuǎn)而成的 C × 該幾何體是由直角梯形繞其下底旋轉(zhuǎn)而成的 D √ 該幾何體是由直角三角形繞其斜邊旋轉(zhuǎn)而成的 答案：D 3．多面體與旋轉(zhuǎn)體 (1)長方體、四面體等，圍成它們的面都是平面的一部分，這樣的幾何體都是多面體．多面體中面與面的交線是直的，它們叫做多面體的棱，棱與棱相交的點(diǎn)叫做多面體的頂點(diǎn)．例如，如圖長方體有12條棱，8個(gè)頂點(diǎn)． (2)圓柱、圓錐、球都是旋轉(zhuǎn)體．圍成圓柱、圓錐的面有平的面和曲的面，其中平的面是底面、曲的面是側(cè)面．圓柱、圓錐中側(cè)

5、面與底面的交線是曲線；圍成球的面是曲的面． 【例3】 下列結(jié)論中正確的是(　　)． ①圓柱由3個(gè)面圍成，這3個(gè)面都是平面； ②圓錐由2個(gè)面圍成，這2個(gè)面中，1個(gè)是平面，1個(gè)是曲面； ③球僅由1個(gè)面圍成，這個(gè)面是平面； ④正方體由6個(gè)面圍成，這6個(gè)面都是平面． A．①② B．②③ C．②④ D．①④ 解析： ① × 圓柱由3個(gè)面圍成，其中兩底面是平面，側(cè)面是曲面，所以①錯(cuò)誤． ② √ 圓錐由2個(gè)面圍成，其中底面是平面，側(cè)面是曲面，所以②正確． ③ × 球是由1個(gè)面圍成的，這個(gè)面是曲面，所以③錯(cuò)誤． ④ √ 正方體是一個(gè)多面體，它是由6個(gè)

6、平面圍成的，所以④正確. 答案：C 釋疑點(diǎn) 對多面體的理解應(yīng)注意的問題 多面體的面都是平面，沒有曲面，可能是規(guī)則的立體圖形，也可能是不規(guī)則的立體圖形．多面體根據(jù)組成這個(gè)立體圖形的面數(shù)決定是幾面體．如正方體是六面體． 4．幾何圖形的有關(guān)概念 (1)幾何圖形中，像直線、角、三角形、圓等，它們上面的各點(diǎn)都在同一個(gè)平面內(nèi)，這樣的圖形叫做平面圖形； (2)像長方體、圓柱體、球等，它們上面的各點(diǎn)不都在同一個(gè)平面內(nèi)，這樣的圖形叫做立體圖形． 【例4】 下面幾種圖形：①三角形；②長方形；③正方體；④圓；⑤圓錐；⑥圓柱．其中屬于立體圖形的是(　　)． A．③⑤⑥ B．①②③ C．③⑥

7、 D．④⑤ 解析：三角形、長方形、正方形、圓是平面圖形；正方體、圓錐、圓柱是立體圖形． 答案：A 釋疑點(diǎn) 正確判斷立體圖形和平面圖形 判斷一個(gè)圖形是立體圖形還是平面圖形，關(guān)鍵是判斷這個(gè)幾何圖形上面的每一個(gè)點(diǎn)是否都在同一個(gè)平面內(nèi)，如果圖形上每一個(gè)點(diǎn)都在同一個(gè)平面內(nèi)，那么這個(gè)幾何圖形就是平面圖形，否則是立體圖形． 5．區(qū)分幾何圖形 幾何體兩種常見分類： 釋疑點(diǎn) 幾何體的分類原則 分類的原則是“不重不漏”．“不重”也就是說同一個(gè)幾何體不能隸屬于同一分類標(biāo)準(zhǔn)下并列的兩個(gè)種類，“不漏”就是說題中所列舉的所有圖形都要能屬于某個(gè)種類． 【例5】 將如圖所示的幾何體進(jìn)行分類，并說

8、明理由． 分析：幾何體的分類不是唯一的．我們應(yīng)先觀察各個(gè)幾何體，努力發(fā)現(xiàn)其共同點(diǎn)，然后可根據(jù)其共同點(diǎn)來進(jìn)行適當(dāng)?shù)姆诸悾? 解：若按柱體、錐體、球體來分類：(2)(3)(5)(6)是柱體，(4)是錐體，(1)是球體； 若按幾何體的面是否含有曲面來分類，則(1)(4)(6)是旋轉(zhuǎn)體，(2)(3)(5)是多面體． 6.探究多面體的棱的條數(shù) 常見的多面體有棱柱和棱錐，判斷一個(gè)多面體的頂點(diǎn)數(shù)和棱數(shù)首先要判斷這個(gè)多面體是棱柱還是棱錐，如果是棱柱，先觀察是幾棱柱，再判斷頂點(diǎn)數(shù)和棱數(shù)，因?yàn)閚棱柱有2n個(gè)頂點(diǎn)，有3n條棱；如果是棱錐，先觀察是幾棱錐，再判斷頂點(diǎn)數(shù)和棱數(shù)，因?yàn)閚棱錐有(n＋1)個(gè)頂點(diǎn)，

9、有2n條棱．對于簡單的棱柱和棱錐也可以根據(jù)圖形的直觀性判斷． 析規(guī)律 多面體的頂點(diǎn)數(shù)、面數(shù)、棱數(shù)之間的關(guān)系 多面體的頂點(diǎn)數(shù)、面數(shù)和棱數(shù)之間存在如下關(guān)系，即頂點(diǎn)數(shù)＋面數(shù)－棱數(shù)＝2，所以一個(gè)多面體只要知道了頂點(diǎn)數(shù)、面數(shù)、棱數(shù)中的任意兩個(gè)可求另一個(gè)數(shù)． 【例6】 如圖所示的八棱柱，它的底面邊長都是5厘米，側(cè)棱長都是6厘米，回答下列問題： (1)這個(gè)八棱柱一共有多少面？它們的形狀分別是什么圖形？哪些面的形狀、面積完全相同？ (2)這個(gè)八棱柱一共有多少條棱？多少個(gè)頂點(diǎn)？ (3)沿一條側(cè)棱將其側(cè)面全部展開成一個(gè)平面圖形，這個(gè)圖形是什么形狀？面積是多少？ 解：(1)這個(gè)八棱柱一共有10個(gè)

10、面，上下兩個(gè)底面是八邊形，八個(gè)側(cè)面都是長方形；上下兩個(gè)底面的形狀、面積完全相同，八個(gè)側(cè)面形狀、面積完全相同． (2)這個(gè)八棱柱一共有24條棱，16個(gè)頂點(diǎn)． (3)沿一條側(cè)棱將其側(cè)面全部展開成一個(gè)平面圖形，這個(gè)圖形是長方形，長為5×8＝40(厘米)，寬為6厘米，所以面積是40×6＝240(平方厘米)． 7．多面體在生活中的應(yīng)用 在現(xiàn)實(shí)生活中，多面體的應(yīng)用十分廣泛，解決生活中的多面體問題，一方面，我們要開動(dòng)腦筋，努力去思考可能會(huì)發(fā)生的多種情況，培養(yǎng)空間想象能力，一題多解問題有利于我們創(chuàng)造性思維的發(fā)展；另一方面，我們要主動(dòng)動(dòng)手操作，在實(shí)踐活動(dòng)中積累經(jīng)驗(yàn)，探索規(guī)律． 通過探究立體圖形的棱的數(shù)量關(guān)系逐步提高同學(xué)們對立體圖形的認(rèn)識，以及數(shù)形結(jié)合的思想． 【例7】 如圖，搭建如圖①的單頂帳篷需要17根鋼管，這樣的帳篷按圖②、圖③的方式串起來搭建，則串7頂這樣的帳篷需要__________根鋼管． 解析：圖①可以看作是一個(gè)正方體和一個(gè)三棱柱組合而成的，它共有17條棱．兩個(gè)這樣的圖形有17×2－6＝28條棱，三個(gè)這樣的圖形有17×3－6×2＝39條棱，…，7個(gè)這樣的圖形有17×7－6×6＝83條棱． 答案：83 4