2022年高考總復習文數(shù)（北師大版）講義：第8章 第03節(jié) 空間中的平行關系 Word版含答案

《2022年高考總復習文數(shù)（北師大版）講義：第8章 第03節(jié) 空間中的平行關系 Word版含答案》由會員分享，可在線閱讀，更多相關《2022年高考總復習文數(shù)（北師大版）講義：第8章 第03節(jié) 空間中的平行關系 Word版含答案（8頁珍藏版）》請在裝配圖網(wǎng)上搜索。

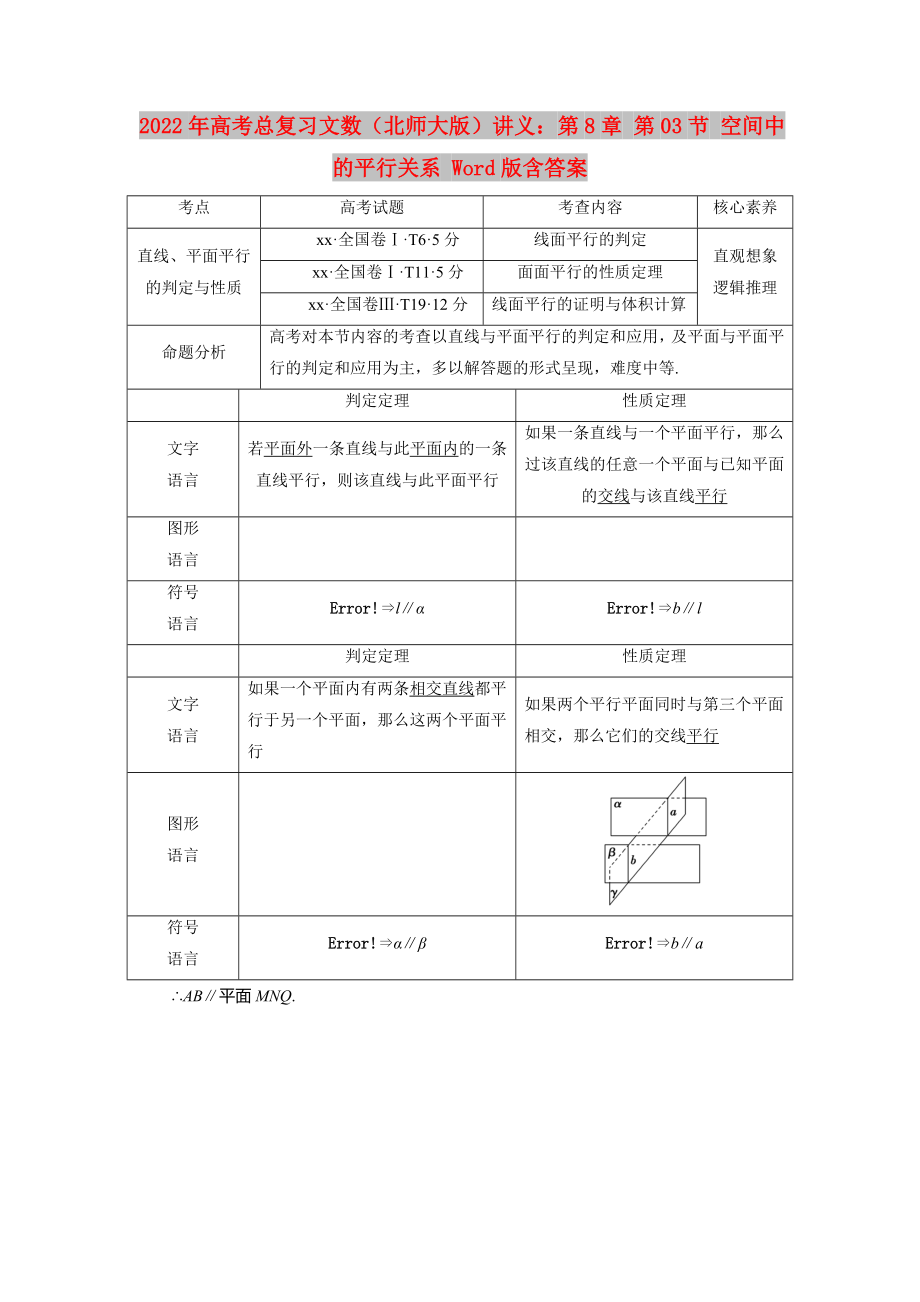
1、2022年高考總復習文數(shù)（北師大版）講義：第8章 第03節(jié) 空間中的平行關系 Word版含答案 考點 高考試題 考查內(nèi)容 核心素養(yǎng) 直線、平面平行 的判定與性質(zhì) 　　xx·全國卷Ⅰ·T6·5分 線面平行的判定 直觀想象 邏輯推理 　　xx·全國卷Ⅰ·T11·5分 面面平行的性質(zhì)定理 　　xx·全國卷Ⅲ·T19·12分 線面平行的證明與體積計算 命題分析 高考對本節(jié)內(nèi)容的考查以直線與平面平行的判定和應用，及平面與平面平行的判定和應用為主，多以解答題的形式呈現(xiàn)，難度中等. 判定定理 性質(zhì)定理 文字 語言 若平面外一條直線與此平面內(nèi)的一條直線平行，則該直

2、線與此平面平行 如果一條直線與一個平面平行，那么過該直線的任意一個平面與已知平面的交線與該直線平行 圖形 語言 符號 語言 ?l∥α ?b∥l 判定定理 性質(zhì)定理 文字 語言 如果一個平面內(nèi)有兩條相交直線都平行于另一個平面，那么這兩個平面平行 如果兩個平行平面同時與第三個平面相交，那么它們的交線平行 圖形 語言 符號 語言 ?α∥β ?b∥a ∴AB∥平面MNQ. C項，作如圖③所示的輔助線，則AB∥CD，CD∥MQ， ∴AB∥MQ.又AB平面MNQ，MQ平面MNQ， ∴AB∥平面MNQ. D項，作如圖④所示的輔助線，則

3、AB∥CD，CD∥NQ. ∴AB∥NQ.又AB平面MNQ，NQ平面MNQ， ∴AB∥平面MNQ.故選A． 4．(教材習題改編)在正方體ABCD －A1B1C1D1中， 點E是DD1的中點， 則BD1與平面ACE的位置關系為________． 解析：連接BD, 設BD∩AC＝O, 連接EO, 在△BDD1中， 點E, O分別是DD1, BD的中點，則EO∥BD1, 又因為EO平面ACE, BD1平面AEC, 所以BD1∥平面ACE. 答案：平行 5．如圖，在空間四邊形ABCD中，M∈AB，N∈AD，若＝，則直線MN與平面BDC的位置關系是________． 解析：在

4、平面ABD中，＝，∴MN∥BD. 又MN平面BCD，BD平面BCD，∴MN∥平面BCD. 答案：平行 直線與平面平行的判定與性質(zhì) [明技法] 證明直線與平面平行的3種方法 (1)定義法：一般用反證法； (2)判定定理法：關鍵是在平面內(nèi)找(或作)一條直線與已知直線平行，證明時注意用符號語言敘述證明過程； (3)性質(zhì)判定法：即兩平面平行時，其中一個平面內(nèi)的任何直線都平行于另一個平面． [提能力] 【典例】 如圖所示，斜三棱柱ABC－A1B1C1中，點D，D1分別為AC，A1C1上的中點． (1)證明AD1∥平面BDC1； (2)證明BD∥平面AB1D1. 證

5、明：(1)∵D1，D分別為A1C1與AC的中點，四邊形ACC1A1為平行四邊形，∴C1D1∥DA，C1D1＝DA， ∴四邊形ADC1D1為平行四邊形，∴AD1∥C1D. 又AD1平面BDC1，C1D平面BDC1， ∴AD1∥平面BDC1. (2)連接D1D. ∵BB1∥平面ACC1A1，BB1平面BB1D1D，平面ACC1A1∩平面BB1D1D＝D1D， ∴BB1∥D1D. 又D1，D分別為A1C1，AC中點，∴BB1＝DD1， ∴四邊形BDD1B1為平行四邊形，∴BD∥B1D1. 又BD平面AB1D1，B1D1平面AB1D1， ∴BD∥平面AB1D1. [母題

6、變式1] 將本例條件“D1，D分別為AC，A1C1上的中點”變?yōu)椤癉1，D分別為AC，A1C1上的點”．試問當?shù)扔诤沃禃r，BC1∥平面AB1D1? 解：如圖，取D1為線段A1C1的中點，此時＝1， 連接A1B交AB1于點O，連接OD1， 由棱柱的性質(zhì)知四邊形A1ABB1為平行四邊形， ∴O為A1B的中點． 在△A1BC1中，點O，D1分別為A1B，A1C1的中點， ∴OD1∥BC1，又OD1平面AB1D1，BC1平面AB1D1， ∴BC1∥平面AB1D1. ∴當＝1時，BC1∥平面AB1D1. [母題變式2] 將本例條件“D，D1分別為AC，A1C1上的中點”變?yōu)椤癉，

7、D1分別為AC，A1C1上的點且平面BC1D∥平面AB1D1”，試求的值． 解：由平面BC1D∥平面AB1D1，且平面A1BC1∩平面BC1D＝BC1，平面A1BC1∩平面AB1D1＝D1O得BC1∥D1O，∴＝. 又＝，＝1，∴＝1，即＝1. 平面與平面平行的判定與性質(zhì) [明技法] 證明面面平行的方法 (1)面面平行的定義； (2)面面平行的判定定理：如果一個平面內(nèi)有兩條相交直線都平行于另一個平面，那么這兩個平面平行； (3)利用垂直于同一條直線的兩個平面平行； (4)兩個平面同時平行于第三個平面，那么這兩個平面平行； (5)利用“線線平行”、“線面平行”、“面面

8、平行”的相互轉(zhuǎn)化． [提能力] 【典例】 如圖所示，在三棱柱ABC－A1B1C1中，E，F(xiàn)，G，H分別是AB，AC，A1B1，A1C1的中點，求證： (1)B，C，H，G四點共面； (2)平面EFA1∥平面BCHG. 解：(1)∵G，H分別是A1B1，A1C1的中點， ∴GH是△A1B1C1的中位線，∴GH∥B1C1. 又∵B1C1∥BC，∴GH∥BC， ∴B，C，H，G四點共面． (2)∵E，F(xiàn)分別是AB，AC的中點，∴EF∥BC. ∵EF平面BCHG，BC平面BCHG， ∴EF∥平面BCHG. ∵A1G∥EB且A1G＝EB， ∴四邊形A1EBG是平行四邊形，

9、∴A1E∥GB. ∵A1E平面BCHG，GB平面BCHG， ∴A1E∥平面BCHG. ∵A1E∩EF＝E， ∴平面EFA1∥平面BCHG. [母題變式1] 在本例條件下，若D為BC1的中點，求證：HD∥平面A1B1BA. 證明：如圖所示，連接HD，A1B， ∵D為BC1的中點，H為A1C1的中點，∴HD∥A1B， 又HD平面A1B1BA，A1B平面A1B1BA， ∴HD∥平面A1B1BA. [母題變式2] 在本例條件下，若D1，D分別為B1C1，BC的中點，求證：平面A1BD1∥平面AC1D. 證明：如圖所示，連接A1C交AC1于點M， ∵四邊形A1ACC1

10、是平行四邊形， ∴M是A1C的中點， 連接MD，∵D為BC的中點， ∴A1B∥DM.∵A1B平面A1BD1，DM平面A1BD1， ∴DM∥平面A1BD1. 又由三棱柱的性質(zhì)知，D1C1BD， ∴四邊形BDC1D1為平行四邊形，∴DC1∥BD1. 又DC1平面A1BD1，BD1平面A1BD1， ∴DC1∥平面A1BD1， 又∵DC1∩DM＝D，DC1，DM平面AC1D， ∴平面A1BD1∥平面AC1D. 直線、平面平行的綜合問題 [明技法] 解決與平行有關的存在性問題的基本策略 先假定題中的數(shù)學對象存在(或結(jié)論成立)，然后在這個前提下進行邏輯推理，若能導出與

11、條件吻合的數(shù)據(jù)或事實，說明假設成立，即存在，并可進一步證明；若導出與條件或?qū)嶋H情況相矛盾的結(jié)果，則說明假設不成立，即不存在． [提能力] 【典例】 一個多面體的直觀圖和三視圖如圖所示，其中M，N分別是AB，AC的中點，G是DF上的一動點． (1)求該多面體的體積與表面積； (2)當點G在什么位置時，有GN∥平面BEF, 給出證明． 解：(1)由題中圖可知該多面體為直三棱柱，在△ADF中，AD⊥DF，DF＝AD＝DC＝a， 所以該多面體的體積為a3，表面積為a2×2＋a2＋a2＋a2＝(3＋)a2. (2)當G是DF的中點時，有GN∥平面BEF, 證明如下： 連接BD. ∵

12、四邊形ABCD是平行四邊形，且N是AC的中點， ∴N是BD的中點，∴GN∥BF， 又BF平面BEF，GN平面BEF， ∴GN∥平面BEF. [母題變式] 當G是DF的中點時，在棱AD上確定一點P，使得GP∥平面FMC，并給出證明． 解：點P與點A重合時，GP∥平面FMC.證明如下： 取FC的中點H，連接GH，GA，MH. ∵G是DF的中點，∴GH∥CD，且GH＝CD. 又M是AB的中點， ∴AM∥CD. AM＝CD. ∴GH∥AM且GH＝AM， ∴四邊形GHMA是平行四邊形．∴GA∥MH. ∵MH平面FMC，GA平面FMC， ∴GA∥平面FMC，即當點P與點A重合時，GP∥平面FMC.