《人教版九年級數(shù)學(xué)下冊:全冊中考知識點(diǎn)梳理-第19講 多邊形與平行四邊形》由會員分享,可在線閱讀���,更多相關(guān)《人教版九年級數(shù)學(xué)下冊:全冊中考知識點(diǎn)梳理-第19講 多邊形與平行四邊形(2頁珍藏版)》請?jiān)谘b配圖網(wǎng)上搜索�。
1�����、..
第五單元 四邊形
第19講 多邊形與平行四邊形
一����、 知識清單梳理
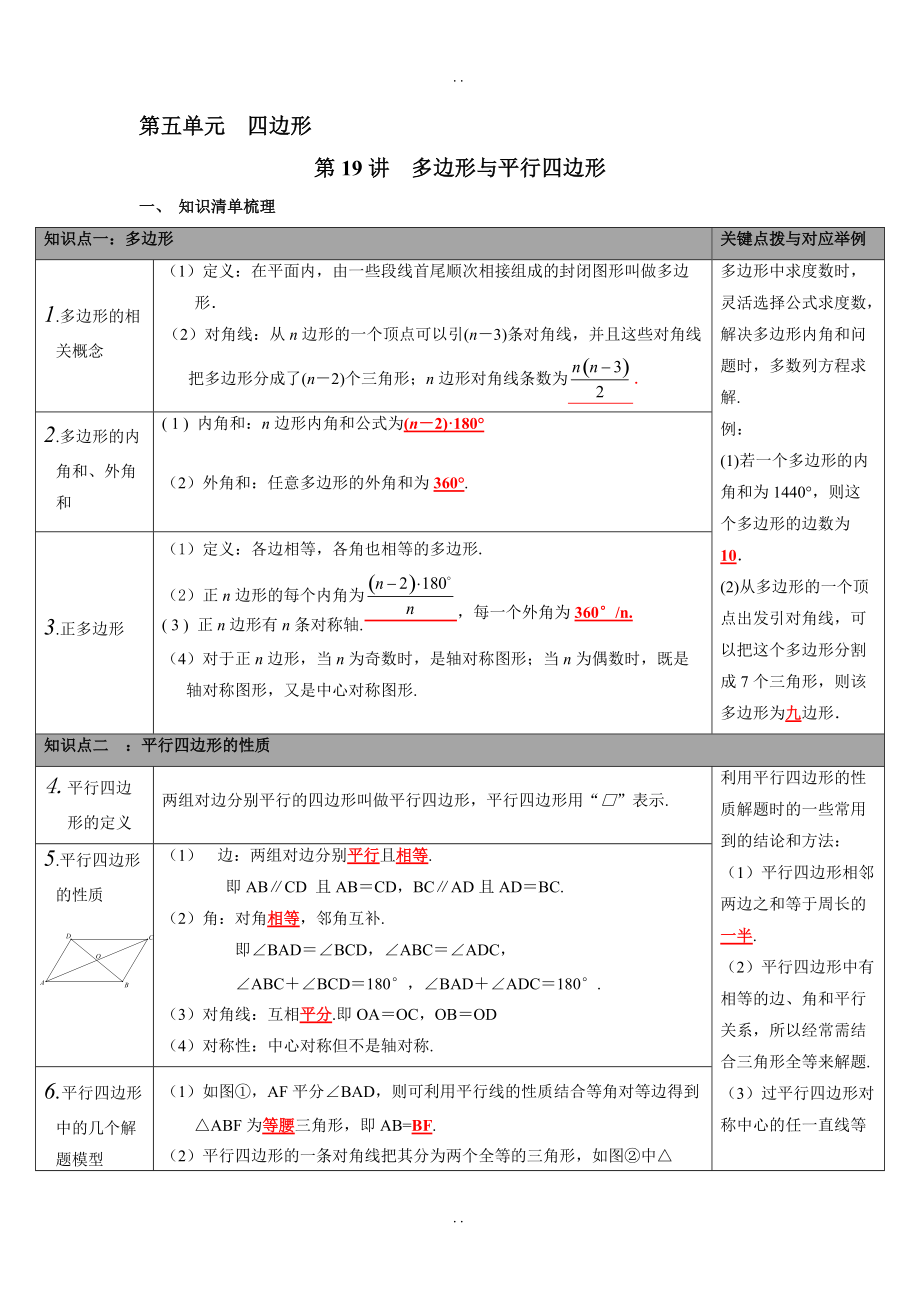
知識點(diǎn)一:多邊形
關(guān)鍵點(diǎn)撥與對應(yīng)舉例
1.多邊形的相關(guān)概念
(1)定義:在平面內(nèi),由一些段線首尾順次相接組成的封閉圖形叫做多邊形.
(2)對角線:從n邊形的一個頂點(diǎn)可以引(n-3)條對角線��,并且這些對角線把多邊形分成了(n-2)個三角形��;n邊形對角線條數(shù)為.
多邊形中求度數(shù)時�,靈活選擇公式求度數(shù),解決多邊形內(nèi)角和問題時�����,多數(shù)列方程求解.
例:
(1)若一個多邊形的內(nèi)角和為1440��,則這個多邊形的邊數(shù)為10.
(2)從多邊形的一個頂點(diǎn)出發(fā)引對角線�,可以把這個多邊形分割成7
2、個三角形�,則該多邊形為九邊形.
2.多邊形的內(nèi)角和、外角和
( 1 ) 內(nèi)角和:n邊形內(nèi)角和公式為(n-2)180
(2)外角和:任意多邊形的外角和為360.
3.正多邊形
(1)定義:各邊相等��,各角也相等的多邊形.
(2)正n邊形的每個內(nèi)角為�,每一個外角為360/n.
( 3 ) 正n邊形有n條對稱軸.
(4)對于正n邊形,當(dāng)n為奇數(shù)時�����,是軸對稱圖形�;當(dāng)n為偶數(shù)時,既是軸對稱圖形�,又是中心對稱圖形.
知識點(diǎn)二 :平行四邊形的性質(zhì)
4.平行四邊形的定義
兩組對邊分別平行的四邊形叫做平行四邊形,平行四邊形用“□”表示.
3����、
利用平行四邊形的性質(zhì)解題時的一些常用到的結(jié)論和方法:
(1)平行四邊形相鄰兩邊之和等于周長的一半.
(2)平行四邊形中有相等的邊、角和平行關(guān)系����,所以經(jīng)常需結(jié)合三角形全等來解題.
(3)過平行四邊形對稱中心的任一直線等分平行四邊形的面積及周長.
例:
如圖,□ABCD中�����,EF過對角線的交點(diǎn)O,AB=4��,AD=3��,OF=1.3�����,則四邊形BCEF的周長為9.6.
5.平行四邊形的性質(zhì)
(1) 邊:兩組對邊分別平行且相等.
即AB∥CD 且AB=CD�,BC∥AD且AD=BC.
(2)角:對角相等,鄰角互補(bǔ).
即∠BAD=∠BCD��,∠ABC=∠AD
4���、C����,
∠ABC+∠BCD=180����,∠BAD+∠ADC=180.
(3)對角線:互相平分.即OA=OC,OB=OD
(4)對稱性:中心對稱但不是軸對稱.
6.平行四邊形中的幾個解題模型
(1)如圖①�,AF平分∠BAD,則可利用平行線的性質(zhì)結(jié)合等角對等邊得到△ABF為等腰三角形�����,即AB=BF.
(2)平行四邊形的一條對角線把其分為兩個全等的三角形��,如圖②中△ABD≌△CDB�����;
兩條對角線把平行四邊形分為兩組全等的三角形��,如圖②中△AOD≌△COB,△AOB≌△COD�����;
根據(jù)平行四邊形的中心對稱性�����,可得經(jīng)過對稱中心O的線段與對角線所組成的居于中心對稱位置的三角形全等���,如圖②△
5�����、AOE≌△COF.圖②中陰影部分的面積為平行四邊形面積的一半.
(3) 如圖③���,已知點(diǎn)E為AD上一點(diǎn)����,根據(jù)平行線間的距離處處相等���,可得S△BEC=S△ABE+S△CDE.
(4) 根據(jù)平行四邊形的面積的求法�����,可得AEBC=AFCD.
知識點(diǎn)三 :平行四邊形的判定
7.平行四邊形的判定
(1)方法一(定義法):兩組對邊分別平行的四邊形是平行四邊形.
即若AB∥CD����,AD∥BC����,則四邊形ABCD是□.
(2)方法二:兩組對邊分別相等的四邊形是平行四邊形.
即若AB=CD,AD=BC���,則四邊形ABCD是□.
(3)方法三:有一組對邊平行且相等的四邊形是平行四邊形.
即若AB=CD�,AB∥CD�,或AD=BC,AD∥BC,則四邊形ABCD是□.
(4)方法四:對角線互相平分的四邊形是平行四邊形.
即若OA=OC,OB=OD��,則四邊形ABCD是□.
(5)方法五:兩組對角分別相等的四邊形是平行四邊形
若∠ABC=∠ADC,∠BAD=∠BCD�����,則四邊形ABCD是□.
例:如圖四邊形ABCD的對角線相交于點(diǎn)O,AO=CO���,請你添加一個條件BO=DO或AD∥BC或AB∥CD(只添加一個即可),使四邊形ABCD為平行四邊形.
..
 人教版九年級數(shù)學(xué)下冊:全冊中考知識點(diǎn)梳理-第19講 多邊形與平行四邊形
人教版九年級數(shù)學(xué)下冊:全冊中考知識點(diǎn)梳理-第19講 多邊形與平行四邊形