人教版 小學9年級 數(shù)學上冊 教案22.1 二次函數(shù)的圖象和性質(zhì)6

《人教版 小學9年級 數(shù)學上冊 教案22.1 二次函數(shù)的圖象和性質(zhì)6》由會員分享，可在線閱讀，更多相關(guān)《人教版 小學9年級 數(shù)學上冊 教案22.1 二次函數(shù)的圖象和性質(zhì)6（3頁珍藏版）》請在裝配圖網(wǎng)上搜索。

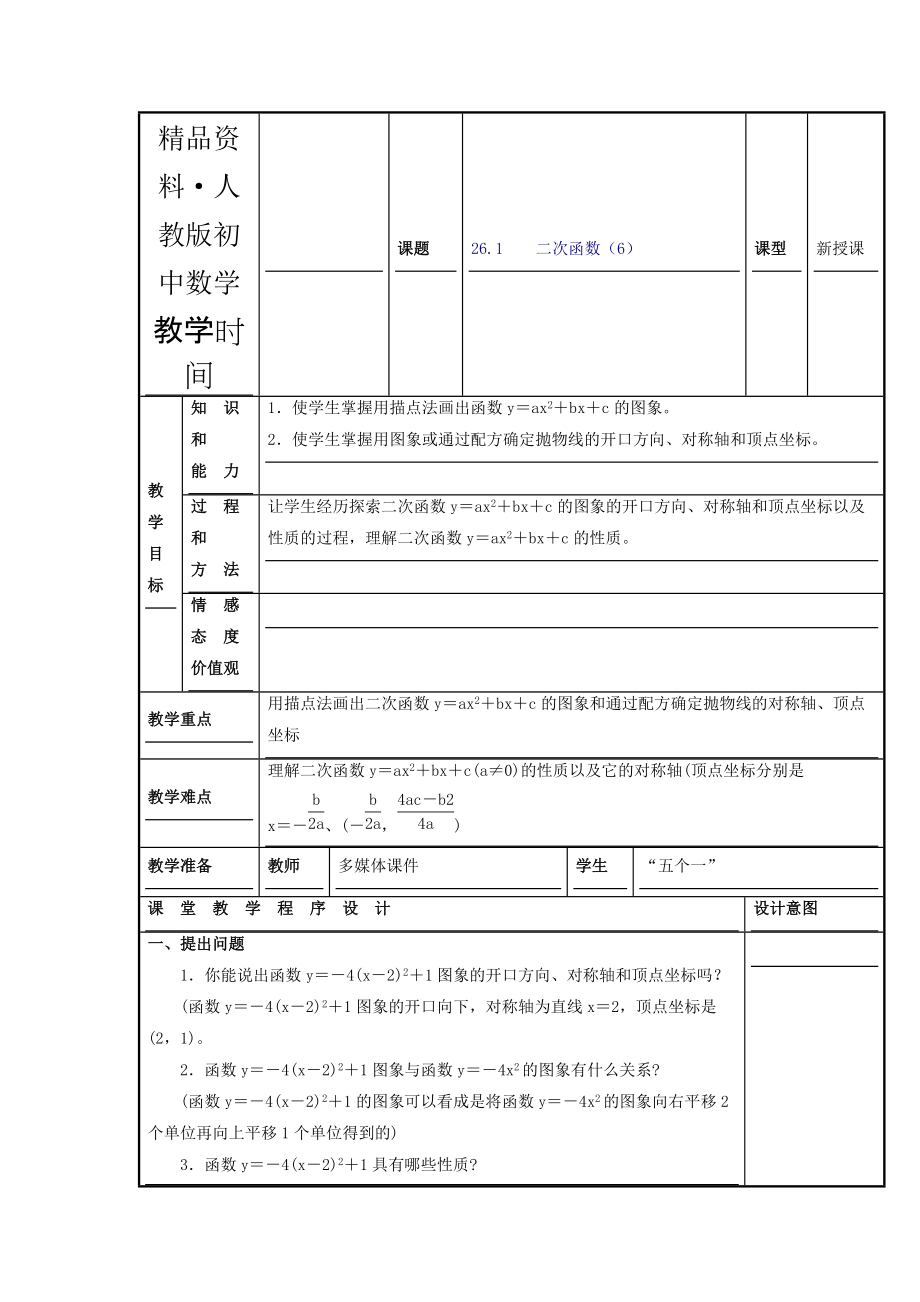
1、精品資料人教版初中數(shù)學 教學時間 課題 26.1　　二次函數(shù)（6） 課型 新授課 教 學 目 標 知　識 和 能　力 1．使學生掌握用描點法畫出函數(shù)y＝ax2＋bx＋c的圖象。 2．使學生掌握用圖象或通過配方確定拋物線的開口方向、對稱軸和頂點坐標。 過　程 和 方　法 讓學生經(jīng)歷探索二次函數(shù)y＝ax2＋bx＋c的圖象的開口方向、對稱軸和頂點坐標以及性質(zhì)的過程，理解二次函數(shù)y＝ax2＋bx＋c的性質(zhì)。 情　感 態(tài)　度 價值觀 教學重點 用描點法畫出二次函數(shù)y＝ax2＋bx＋c的圖象和通過配方確定拋物線的對稱軸、頂點坐標 教學難點 理解二次

2、函數(shù)y＝ax2＋bx＋c(a≠0)的性質(zhì)以及它的對稱軸(頂點坐標分別是x＝－、(－，) 教學準備 教師 多媒體課件 學生 “五個一” 課 堂 教 學 程 序 設(shè) 計 設(shè)計意圖 一、提出問題 1．你能說出函數(shù)y＝－4(x－2)2＋1圖象的開口方向、對稱軸和頂點坐標嗎？ (函數(shù)y＝－4(x－2)2＋1圖象的開口向下，對稱軸為直線x＝2，頂點坐標是(2，1)。 2．函數(shù)y＝－4(x－2)2＋1圖象與函數(shù)y＝－4x2的圖象有什么關(guān)系? (函數(shù)y＝－4(x－2)2＋1的圖象可以看成是將函數(shù)y＝－4x2的圖象向右平移2個單位再向上平移1

3、個單位得到的) 3．函數(shù)y＝－4(x－2)2＋1具有哪些性質(zhì)? (當x＜2時，函數(shù)值y隨x的增大而增大，當x＞2時，函數(shù)值y隨x的增大而減??；當x＝2時，函數(shù)取得最大值，最大值y＝1) 4．不畫出圖象，你能直接說出函數(shù)y＝－x2＋x－的圖象的開口方向、對稱軸和頂點坐標嗎? [因為y＝－x2＋x－＝－(x－1)2－2，所以這個函數(shù)的圖象開口向下，對稱軸為直線x＝1，頂點坐標為(1，－2)] 5．你能畫出函數(shù)y＝－x2＋x－的圖象，并說明這個函數(shù)具有哪些性質(zhì)嗎? 二、解決問題 由以上第4個問題的解決，我們已經(jīng)知道函數(shù)y＝－x2＋x－的圖

4、象的開口方向、對稱軸和頂點坐標。根據(jù)這些特點，可以采用描點法作圖的方法作出函數(shù)y＝－x2＋x－的圖象，進而觀察得到這個函數(shù)的性質(zhì)。 說明：(1)列表時，應(yīng)根據(jù)對稱軸是x＝1，以1為中心，對稱地選取自變量的值，求出相應(yīng)的函數(shù)值。相應(yīng)的函數(shù)值是相等的。 (2)直角坐標系中x軸、y軸的長度單位可以任意定，且允許x軸、y軸選取的長度單位不同。所以要根據(jù)具體問題，選取適當?shù)拈L度單位，使畫出的圖象美觀。 讓學生觀察函數(shù)圖象，發(fā)表意見，互相補充，得到這個函數(shù)韻性質(zhì)； 當x＜1時，函數(shù)值y隨x的增大而增大；當x＞1時，函數(shù)值y隨x的增大而減??； 當x＝1時，函數(shù)取得最大值，最

5、大值y＝－2 三、做一做 1．請你按照上面的方法，畫出函數(shù)y＝x2－4x＋10的圖象，由圖象你能發(fā)現(xiàn)這個函數(shù)具有哪些性質(zhì)嗎? 教學要點 (1)在學生畫函數(shù)圖象的同時，教師巡視、指導(dǎo)； (2)叫一位或兩位同學板演，學生自糾，教師點評。 2．通過配方變形，說出函數(shù)y＝－2x2＋8x－8的圖象的開口方向、對稱軸和頂點坐標，這個函數(shù)有最大值還是最小值?這個值是多少? 教學要點 (1)在學生做題時，教師巡視、指導(dǎo)；(2)讓學生總結(jié)配方的方法；(3)讓學生思考函數(shù)的最大值或最小值與函數(shù)圖象的開口方向有什么關(guān)系?這個值與函數(shù)圖象的頂點坐

6、標有什么關(guān)系? 以上講的，都是給出一個具體的二次函數(shù)，來研究它的圖象與性質(zhì)。那么，對于任意一個二次函數(shù)y＝ax2＋bx＋c(a≠0)，如何確定它的圖象的開口方向、對稱軸和頂點坐標?你能把結(jié)果寫出來嗎? 教師組織學生分組討論，各組選派代表發(fā)言，全班交流，達成共識； y＝ax2＋bx＋c＝a(x2＋x)＋c ＝a[x2＋x＋()2－()2]＋c ＝a[x2＋x＋()2]＋c－ ＝a(x＋)2＋ 當a＞0時，開口向上，當a＜0時，開口向下。對稱軸是x＝－b/2a，頂點坐標是(－，) 四、課堂練習：　　P12練習。 五、小結(jié)：　通過本節(jié)課的學習，你學到了什么知識？有何體會？ 作業(yè) 設(shè)計 必做 教科書P14：6 選做 教科書P15：12 教學 反思