《【導(dǎo)與練】新課標(biāo)高三數(shù)學(xué)一輪復(fù)習(xí) 第5篇 等比數(shù)列及其前n項和學(xué)案 理》由會員分享�����,可在線閱讀,更多相關(guān)《【導(dǎo)與練】新課標(biāo)高三數(shù)學(xué)一輪復(fù)習(xí) 第5篇 等比數(shù)列及其前n項和學(xué)案 理(6頁珍藏版)》請在裝配圖網(wǎng)上搜索�。
1、第三十四課時 等比數(shù)列
課前預(yù)習(xí)案
考綱要求
1.理解等比數(shù)列的概念����;
2.掌握等比數(shù)列的通項公式與前n項和公式;
3.能在具體的問題情境中識別數(shù)列的等比關(guān)系.
4.了解等比數(shù)列與指數(shù)函數(shù)的關(guān)系.
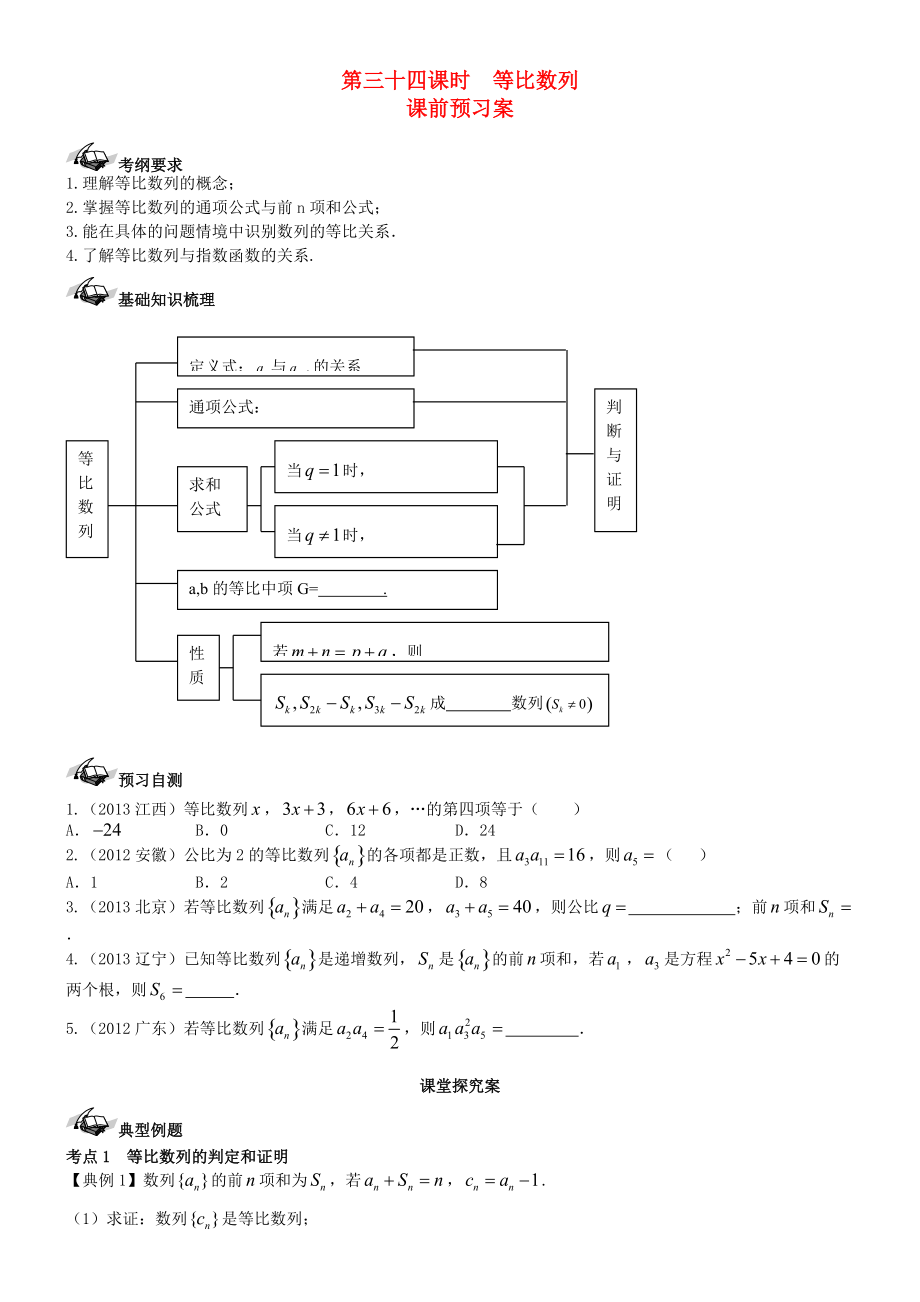
基礎(chǔ)知識梳理
等比數(shù)列
定義式:與的關(guān)系
通項公式:
求和
公式
a,b的等比中項G= .
性質(zhì)
若��,則
成 數(shù)列
判斷與證明
當(dāng)時�,
當(dāng)時,
預(yù)習(xí)自測
1.(2013江西)等比數(shù)列��,���,���,…的第四項等于( )
A. B.0 C.12 D.24
2.(2012安徽)公比為2的等比數(shù)列的各項都是
2、正數(shù)���,且���,則( )
A.1 B.2 C.4 D.8
3.(2013北京)若等比數(shù)列滿足��,��,則公比 ;前項和 .
4.(2013遼寧)已知等比數(shù)列是遞增數(shù)列��,是的前項和���,若���,是方程的兩個根,則 .
5.(2012廣東)若等比數(shù)列滿足���,則 .
課堂探究案
典型例題
考點(diǎn)1 等比數(shù)列的判定和證明
【典例1】數(shù)列的前項和為����,若���,.
(1)求證:數(shù)列是等比數(shù)列���;
(2)并求數(shù)列的通項公式.
【變式1】 在數(shù)列中,.
(1)證明數(shù)列是等比數(shù)列�;
(2)求數(shù)列的通項公式.
考點(diǎn)2 等比數(shù)列的通
3�、項和求和公式
【典例2】等比數(shù)列滿足:����,,且公比.
(1)求數(shù)列的通項公式��;
(2)若該數(shù)列前項和���,求的值.
【變式2】 (2013年天津)已知首項為的等比數(shù)列的前項和為()�,且���,�����,成等差數(shù)列.
(1)求數(shù)列的通項公式�;
(2)證明:().
考點(diǎn)3 等比數(shù)列的性質(zhì)的應(yīng)用
【典例3】(1)在等比數(shù)列中����,已知,���, = .
(2)已知各項均為正數(shù)的等比數(shù)列�,,�,則____
(3)在等比數(shù)列中,���,�,則 .
【變式3】【2012高考安徽】公比為2的等比數(shù)列{} 的各項都是正數(shù)�,且 =16�,則=( )
A. 1 B.
4、2 C . 4 D. 8
當(dāng)堂檢測
1.在等比數(shù)列中�����,如果公比�����,那么等比數(shù)列是( ).
A.遞增數(shù)列 B.遞減數(shù)列 C.常數(shù)列 D.無法確定數(shù)列的增減性
2.已知等比數(shù)列的公比為正數(shù)���,且=2��,=2����,則=( )
A. B. C. D.2
3. (2012大綱全國)已知數(shù)列的前項和為,�����,�,則( )
A. B. C. D.
4.(2013新課標(biāo)II)等比數(shù)列的前項和為,已知���,���,則( )
A. B. C. D.
課后拓展案
A組全員
5、必做題
1. 等比數(shù)列{}中�����,��,則=( )
A.9 B. C. D.
2.(2012北京)已知為等比數(shù)列�����,下面結(jié)論中正確的是( )
A. B. C.若���,則 D.若�,則
3. 設(shè)是有正數(shù)組成的等比數(shù)列,為其前項和,已知,,則( )
A. B. C. D.
4.在等比數(shù)列中����,若,�����,則公比 .
5.在等比數(shù)列{an}中�,若a1=���,a4=-4����,則公比q=________�;
|a1|+|a2|+…+|an|=________.
6、B組提高選做題
1.(2012江西)等比數(shù)列的前項和為��,公比不為1.若��,則對任意的���,都有�,則 .
2.已知數(shù)列滿足,����,,.
(1)令�,證明:是等比數(shù)列;(2)若是的前n項和�����,求證1.
參考答案
預(yù)習(xí)自測
1.A
2.A
3.2
4.63
5.
典型例題
【典例1】(1)證明:�����,故��,
∴��,�,
∴,即.
又��,
∴數(shù)列為等比數(shù)列��,首項為,公比為.
(2)解:由(1)知��,
.
∴.
【變式1】(1)證明:�����,故����,
又∵,∴數(shù)列為等比數(shù)列.
(2)解:由(1)知�����,��,∴.
【典例2】解:(1)����,又�,
∴或
又,
∴���,�,���,
∴.
(2)����,解得.
【變式2】(1)解:設(shè)等比數(shù)列的公比為q,由題意����,
∴,
∴���,
∴�,.
(2)證明:=1-�����,
∴
為奇數(shù)時���,遞減�,∴��;
為偶數(shù)時�����,遞減,∴.
∴����,有.
【典例3】(1);(2)��;(3)63
【變式3】A
當(dāng)堂檢測
1.D
2.C
3.B
4.C
A組全員必做題
1.A
2.B
3.B
4.2
5.�����;
B組提高選做題
1.11
2.(1)證明:���,
且�����,
∴數(shù)列為等比數(shù)列.
(2)
由(1)得===
當(dāng)時���,<,
當(dāng)時�����,=1.
所以1.
 【導(dǎo)與練】新課標(biāo)高三數(shù)學(xué)一輪復(fù)習(xí) 第5篇 等比數(shù)列及其前n項和學(xué)案 理
【導(dǎo)與練】新課標(biāo)高三數(shù)學(xué)一輪復(fù)習(xí) 第5篇 等比數(shù)列及其前n項和學(xué)案 理